Soit $f$ la fonction définie par :

$$f(x)=\begin{cases}x\,\arctan\left(\frac{1}{x}\right) \,\,\,\,\,&\text{Si}\,x\neq 0\\ 0\,\qquad &\text{Si}\,x=0 \end{cases}$$

On note $\mathcal{C}_f$ sa courbe représentative dans un repère orthonormé.

 

1. $f$ est-elle continue sur $\mathbb{R}$ ?

2. $f$ est-elle dérivable sur $\mathbb{R}$ ?

3. Déterminer la limite : $\displaystyle\lim_{x\to +\infty}f(x)$

4. Montrer que pour tout réel $x$ strictement positif, on a :

$$\frac{x}{x^2+1}<\arctan\left(\frac{1}{x}\right)$$

5. En déduire le sens de variation de $f$ sur $\mathbb{R}$ et dresser son tableau de variations.

6. Donner les équations des demi-tangentes à la courbe $\mathcal{C}_f$ au point d’abscisse $0$.

7. Tracer la courbe $\mathcal{C}_f$.

 

FIN

$f$ est la fonction définie par :

$$f(x)=\begin{cases}x\,\arctan\left(\frac{1}{x}\right) \,\,\,\,\,&\text{Si}\,x\neq 0\\ 0\,\qquad &\text{Si}\,x=0 \end{cases}$$

$\mathcal{C}_f$ est sa courbe représentative dans un repère orthonormé.

 

1. Etude de la continuité de $f$ :

Pour $x\neq 0$, $f(x)=x\,\arctan\left(\frac{1}{x}\right)$ :

$f$ est le produit des fonctions $x\mapsto x$ et de $x\mapsto\arctan\left(\frac{1}{x}\right)$.

La fonction $x\mapsto\arctan\left(\frac{1}{x}\right)$ est la composée de $\displaystyle x\mapsto\frac{1}{x}$ continue sur $\mathbb{R}^*$ et de $x\mapsto\arctan(x)$ continue sur $\mathbb{R}^*$. Donc par composition, $x\mapsto\arctan\left(\frac{1}{x}\right)$ est continue sur $\mathbb{R}^*$.

Comme la fonction $x\mapsto x$ est continue sur $\mathbb{R}^*$, alors par produit $f$ est continue sur $\mathbb{R}^*$.

 

Pour $x=0$ :

$f$ est continue en $0$ si et seulement si $\displaystyle\lim_{x\to 0}f(x)=f(0)$

La fonction $x\mapsto\arctan\left(\frac{1}{x}\right)$ est la composée de $\displaystyle x\mapsto\frac{1}{x}$ et de $X\mapsto\arctan(X)$.

Puisque la limite $\displaystyle\lim_{x\to 0}\frac{1}{x}=\pm\infty$ selon que $x$ tende vers $0$ par la droite ou par la gauche, alors il convient de considérer ces deux cas séparément.

 

Cas N° 1 : $x$ est strictement positif

On a $\displaystyle\lim_{x\to 0^+}\frac{1}{x}=+\infty$ et $\displaystyle\lim_{X\to +\infty}\arctan(x)=\frac{\pi}{2}$, on peut donc écrire $\displaystyle\lim_{x\to 0^+}\arctan\left(\frac{1}{x}\right)=\lim_{X\to +\infty}\arctan(X)=\frac{\pi}{2}$ par composition avec $\displaystyle X=\frac{1}{x}$.

D’où par produit,

$\displaystyle\lim_{x\to 0^+}f(x)=\lim_{x\to 0^+}x\,\arctan\left(\frac{1}{x}\right)=0=f(0)$

 

Cas N° 2 : $x$ est strictement négatif

De la même manière que pour le cas N° 1, on a :

$\displaystyle\lim_{x\to 0^-}\frac{1}{x}=-\infty$ et $\displaystyle\lim_{X\to -\infty}\arctan(x)=-\frac{\pi}{2}$, on peut donc écrire $\displaystyle\lim_{x\to 0^-}\arctan\left(\frac{1}{x}\right)=\lim_{X\to -\infty}\arctan(X)=-\frac{\pi}{2}$ par composition avec $\displaystyle X=\frac{1}{x}$.

D’où par produit,

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^-}x\,\arctan\left(\frac{1}{x}\right)=0=f(0)$

 

Les deux limites de $f$ à gauche et à droite de $0$ existent et sont égales à $0=f(0)$. On en déduit que $f$ est continue en zéro et $f(0)=0\,$.

 

2. Etude de la dérivabilité de $f$ :

Pour $x\neq 0$, $f(x)=x\,\arctan\left(\frac{1}{x}\right)$ :

$f$ est le produit des fonctions $x\mapsto x$ et de $x\mapsto\arctan\left(\frac{1}{x}\right)$.

La fonction $x\mapsto\arctan\left(\frac{1}{x}\right)$ est la composée de $\displaystyle x\mapsto\frac{1}{x}$ dérivable sur $\mathbb{R}^*$ et de $x\mapsto\arctan(x)$ dérivable sur $\mathbb{R}^*$. Donc par composition, $x\mapsto\arctan\left(\frac{1}{x}\right)$ est dérivable sur $\mathbb{R}^*$.

Comme la fonction $x\mapsto x$ est dérivable sur $\mathbb{R}^*$, alors par produit $f$ est dérivable sur $\mathbb{R}^*$.

 

Pour $x=0$ :

$f$ est dérivable en $0$ si le taux si et seulement si le taux d’accroissement $\displaystyle\frac{f(x)-f(0)}{x-0}$ admet une limite finie lorsque $x$ tend vers $0$.

Soit $x$ un réel de $\mathbb{R}^*$. On a :

$\displaystyle\frac{f(x)-f(0)}{x-0}=\arctan\left(\frac{1}{x}\right)$

Or la limite $\displaystyle\lim_{x\to 0}\arctan\left(\frac{1}{x}\right)$ a été calculée dans la question 1 et on a :

$\displaystyle\lim_{x\to 0^+}\arctan\left(\frac{1}{x}\right)=\frac{\pi}{2}$ et $\displaystyle\lim_{x\to 0^-}\arctan\left(\frac{1}{x}\right)=-\frac{\pi}{2}$

 

Le taux d’accroissement $\displaystyle\frac{f(x)-f(0)}{x-0}$ n’admet pas de limite lorsque $x$ tend vers $0$ (limite à droite de $0$ différente de la limite à gauche de $0$), par conséquent $f$ n’est pas dérivable en $0$.

En revanche, comme les limites $\displaystyle\lim_{x\to 0^+}\frac{f(x)-f(0)}{x-0}$ et $\displaystyle\lim_{x\to 0^-}\frac{f(x)-f(0)}{x-0}$ existent et valent respectivement $\displaystyle \frac{\pi}{2}$ et $\displaystyle -\frac{\pi}{2}\,$, alors $f$ est dérivable à droite de $0$ et à gauche de $0$.

 

3. Déterminer la limite : $\displaystyle\lim_{x\to +\infty}f(x)$

Soit $x$ un réel strictement positif (ici on est au voisinage de $+\infty$ ) :

On a,

$\displaystyle\begin{align}f(x)&=x\,\arctan\left(\frac{1}{x}\right)\\&=\frac{\arctan\left(\frac{1}{x}\right)}{\frac{1}{x}}\end{align}$

Cette écriture suggère de procéder par changement de variable en posant $\displaystyle u=\frac{1}{x}$, ainsi lorsque $x$ tend vers $+\infty$, $u$ tend vers $0$ par la droite et on a :

$\displaystyle\begin{align}\lim_{x\to +\infty}f(x)&=\lim_{x\to +\infty}\frac{\arctan\left(\frac{1}{x}\right)}{\frac{1}{x}}\\&=\lim_{u\to 0}\frac{\arctan(u)}{u}\\&=1\end{align}$

C’est en effet une limite connue et selon le contexte, vous pouvez soit donner le résultat directement soit le démontrer.

Voici une proposition de démonstration :

$\displaystyle\lim_{x\to 0}\frac{\arctan(x)}{x}=\lim_{x\to 0}\frac{g(x)-g(0)}{x-0}$ où $g(x)=\arctan(x)$. Or $g$ est dérivable sur $\mathbb{R}$ et a fortiori en $0$, donc le taux d’accroissement $\displaystyle\frac{g(x)-g(0)}{x-0}$ admet une limite finie en $0$ et on a,

$\displaystyle\begin{align}\lim_{x\to 0}\frac{g(x)-g(0)}{x-0}&=g^{\prime}(0)\\&=\frac{1}{1+0^2}\\&=1\end{align}$

 

La limite $\displaystyle\lim_{x\to +\infty}f(x)$ existe et est égale à $1$. Géométriquement, on dit que la courbe $\mathcal{C}_f$ admet une asymptote horizontale d’équation $y=1$.

 

4. Montrer que pour tout réel $x$ strictement positif, on a :

$$\frac{x}{x^2+1}<\arctan\left(\frac{1}{x}\right)$$

Posons $g$ la fonction définie sur $\mathbb{R}_+^*$ par :

$\displaystyle g(x)=\frac{x}{x^2+1}-\arctan\left(\frac{1}{x}\right)$

 

Pour montrer l’inégalité demandée, il suffit de montrer que pour tout réel $x$ dans $\mathbb{R}_+^*\,$, $g(x)<0$.

La connaissance des variations de $g$ permet de répondre à cette question.

$g$ est dérivable sur $\mathbb{R}_+^*$ comme somme de deux fonctions dérivables sur $\mathbb{R}_+^*$ et pour tout réel $x$ strictement positif, on a :

$$\begin{align}g^{\prime}(x)&=\frac{1\times (x^2+1)-2x\times x}{(x^2+1)^2}-\frac{-\frac{1}{x^2}}{1+\frac{1}{x^2}}\\&=\frac{1-x^2}{(x^2+1)^2}+\frac{1}{x^2+1}\\\\&=\frac{2}{(x^2+1)^2}\end{align}$$

Donc pour tout réel $x$ strictement positif, $g^{\prime}(x) > 0$ et $g$ est strictement croissante sur $\mathbb{R}_+^*$.

Par ailleurs,

$$\begin{align}\lim_{x\to 0^+}g(x)&=\lim_{x\to 0^+}\left(\frac{x}{x^2+1}-\arctan\left(\frac{1}{x}\right)\right)\\&=\lim_{x\to 0^+}\frac{x}{x^2+1}-\lim_{x\to 0^+}\arctan\left(\frac{1}{x}\right)\end{align}$$

Or, $\displaystyle\lim_{x\to 0^+}\frac{x}{x^2+1}=0$ et $\displaystyle\lim_{x\to 0^+}\arctan\left(\frac{1}{x}\right)=\frac{\pi}{2}$ d’après la question 1, on en déduit que,

$\displaystyle\lim_{x\to 0^+}g(x)=-\frac{\pi}{2}$

Et $\displaystyle\lim_{x\to +\infty}g(x)=0$ car,

$\displaystyle\lim_{x\to +\infty}\frac{x}{x^2+1}=0$ car une fonction rationnelle a les mêmes limites que le quotient des monômes de plus haut degré du numérateur et du dénominateur puis on conclut par quotient.

Et $\displaystyle\lim_{x\to +\infty}\arctan\left(\frac{1}{x}\right)=\lim_{u\to 0^+}\arctan(u)=0$.

Comme $g$ est continue (car dérivable) et strictement croissante sur $\mathbb{R}_+^*$, alors $\displaystyle g\left(\mathbb{R}_+^*\right)=\left]-\frac{\pi}{2}\,;\,0\right[$ et pour tout réel $x$ strictement positif, on a $g(x) < 0$ et par suite $\displaystyle\frac{x}{x^2+1}<\arctan\left(\frac{1}{x}\right)$.

 

Remarque :

Comme on sait que $g$ est continue et strictement croissante sur $\mathbb{R}_+^*\,$, le calcul de la limite $\displaystyle\lim_{x\to +\infty}g(x)$ aura suffi pour conclure.

 

5. Tableau de variations de $f$ sur $\mathbb{R}$ :

Pour connaître les variations de $f$ sur $\mathbb{R}$, il faudra commencer par déterminer la dérivée de $f$ puis étudier son signe.

$f$ est dérivable sur $\mathbb{R}_+^*$ (voir question 2) et pour tout réel $x$ de $\mathbb{R}_+^*$ on a :

$\displaystyle\begin{align}f^{\prime}(x)&=\arctan\left(\frac{1}{x}\right)+x\times -\frac{1}{x^2}\times\frac{1}{1+\frac{1}{x^2}}\\&=\arctan\left(\frac{1}{x}\right)-\frac{x}{x^2+1}\end{align}$

On déduit grâce à la question précédente que pour tout réel $x$ dans $\mathbb{R}_+^*$, $f^{\prime}(x)>0$ et $f$ est strictement croissante sur $\mathbb{R}_+^*$.

Par ailleurs, $f$ est paire car,

La fonction $\displaystyle x\mapsto\frac{1}{x}$ est impaire et la fonction $\displaystyle x\mapsto\arctan(x)$ est impaire, donc par composition, la fonction $\displaystyle x\mapsto\arctan\left(\frac{1}{x}\right)$ est impaire.

$f$ est définie sur $\mathbb{R}$ et $\forall x\in\mathbb{R}$, on a $-x\in\mathbb{R}$.

Soit $x\in\mathbb{R}$, on a :

$\displaystyle\begin{align}f(-x)&=-x\arctan\left(-\frac{1}{x}\right)\\&=x\arctan\left(\frac{1}{x}\right)\\&=f(x)\end{align}$

$f$ est paire donc symétrique par rapport à l’axe des ordonnées. Puisque $f$ est strictement croissante sur $\mathbb{R}_+^*$, alors par symétrie, $f$ est strictement décroissante sur $\mathbb{R}_-^*$ et $\displaystyle\lim_{x\to -\infty}f(x)=\lim_{x\to +\infty}f(x)=1$.

 

D’où le tableau de variations de $f$ :

$$\displaystyle\begin{array}{|c|lcccr|} \hline x & -\infty\qquad&&\qquad 0 \qquad &&\qquad +\infty \\ \hline \text{Signe de } f^{\prime} &&&+&&\\ \hline \hline &1&&&&1\\ \text{Variations de } f &&\searrow&&\nearrow&\\&&&0&&\\ \hline \end{array}$$

 

6. Équations des demi-tangentes à la courbe $\mathcal{C}_f$ au point d’abscisse $0$ :

On a vu à la question 2 que $f$ est dérivable à droite de $0$ et à gauche de $0$ mais pas en $0$. La courbe $\mathcal{C}_f$ admet deux demi-tangentes de part et d’autres de $0$.

Une équation de la demi-tangete à $\mathcal{C}_f$ à droite de $0$ est donnée par : $\displaystyle y=f^{\prime}_d(0)(x-0)+f(0)$ soit $\displaystyle y=\frac{\pi}{2}x$.

Une équation de la demi-tangete à $\mathcal{C}_f$ à gauche de $0$ est $\displaystyle y=-\frac{\pi}{2}x$.

7. Représentation graphique de la courbe $\mathcal{C}_f$ :

 

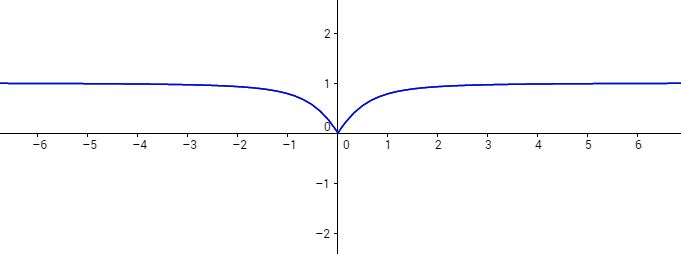
FIN