Dans cet article, je propose de revenir sur la notion de limite d’une fonction en un point à travers des situations simples, mais qui restent parfois peu assimilées.
J’espère que cet article vous aidera en classe de terminale.
Bonne lecture ![]()
Soit $f$ la fonction définie par :
$$f\,:\begin{cases}x-1\qquad\qquad\text{si }x\neq 2\\\text{indéfinie}\qquad\,\,\,\text{si }x=2\end{cases}$$
La représentation graphique de $f$ dans un repère orthonormé est :
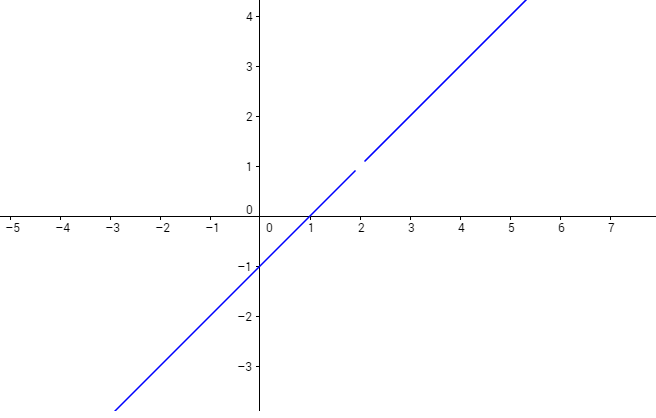
Question :
Comment se comporte $f$ lorsque $x$ se rapproche de $2$ ? $x$ se rapproche de $2$ d’aussi près que l’on veut.
Imaginons que ce graphique représente une montagne avec un trou au point d’abscisse $x=2$.
Vous êtes en train d’escalader la montagne, vous grimpez, vous contrôlez votre hauteur $h$ à tout moment.
À titre indicatif, on a :
$h(0)=-1$
$h(1)=0$
$h(1,5)=0,5$
$h(1,9)=0,9$
$h(1,9999)=0,9999$
Vous grimpez, vous vous approchez du trou ($h=1$), vous pouvez vous en approcher d’aussi près que vous le voudriez, mais vous n’atteindrez jamais la hauteur $h=1$ parce qu’il y a un trou à ce niveau.
Autrement reformulé, lorsque $x$ est très proche de $2$ mais n’est pas égal à $2$, la hauteur $h$ est très proche de $1$ et on écrit,
$$\lim_{x\to 2}f(x)=1$$
Attention :
La limite (ci-dessus) lorsque $x$ tend vers $2$ ne signifie pas que $x=2$.
Ainsi, la fonction $\displaystyle x\mapsto\frac{x^2-1}{x-1}$ n’est pas définie en $x=1$, mais on peut calculer la limite : $\displaystyle\lim_{x\to 1}\frac{x^2-1}{x-1}$.
En effet, pour tout réel $x\neq 1$, on a :
$$\begin{align}\frac{x^2-1}{x-1}&=\frac{(x-1)(x+1)}{x-1}\\&=x+1\end{align}$$
D’où,
$$\begin{align}\lim_{x\to 1}\frac{x^2-1}{x-1}&=\lim_{x\to 1} x+1\\&=2\end{align}$$
Parce que la limite lorsque $x$ tend vers $1$ signifie que $x$ est proche de $1$, aussi proche que l’on veut, mais il n’est pas égal à $1$.
Remarque 1 :
Soit $g$ la fonction définie par :
$$g\,:\begin{cases}x-1\qquad\qquad\,\text{si }x\neq 2\\3\qquad\qquad\qquad\text{si }x=2\end{cases}$$La représentation graphique de $g$ dans un repère orthonormé est la suivante :
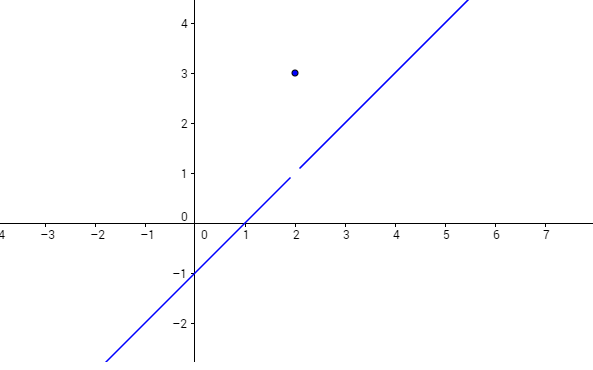
Quelle est la limite de $g$ lorsque $x$ tend vers 2 ?
D’après la définition de $g$, nous avons $g(2)=3$, mais la limite lorsque $x$ se rapproche de $2$ ne signifie pas $x=2$. On ne se préoccupe pas de ce qui se passe au point $x=2$.
Ainsi, lorsque $x$ devient très proche de $2$, $g$ est très proche de 1. Donc,
$$\lim_{x\to 2}g(x)=1$$
Remarque 2 :
Soit $h$ la fonction dont la représentation graphique est la suivante :
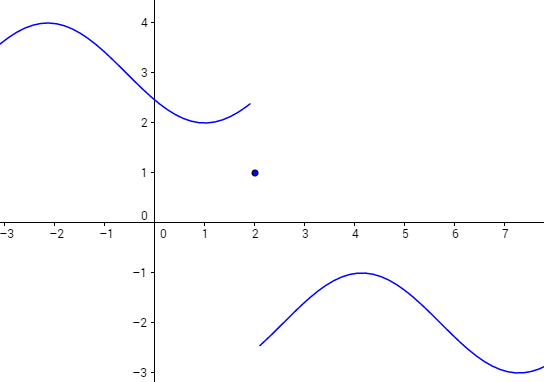
Quelle est la limite de $h$ lorsque $x$ tend vers $2$ ?
À la lecture du graphique ci-dessus, on sait que lorsque $x$ se rapproche de $2$ par la gauche ($x<2$), $h$ s’approche de $2,5$. Ainsi,
$$\lim_{\substack{x\to 2 \\ x<2}}h(x)=2,5$$
Et lorsque $x$ tend vers $2$ par la droite ($x>2$), $h$ s’approche de $-2,5$. Ainsi,
$$\lim_{ \substack{x\to 2 \\ x>2}}h(x)=-2,5$$
Mais quelle est la limite de $\displaystyle\lim_{x\to 2}h(x)$ ?
Ici, nous avons,
$$\lim_{ \substack{x\to 2 \\ x<2}}h(x)\neq\lim_{ \substack{x\to 2 \\ x>2}}h(x)$$
Donc, la limite de $h$ en $2$ n’existe pas car les deux limites de $h$ à gauche de $2$ est à droite de $2$ sont différentes.
Généralisation :
Soit $a$ un réel et soit $f$ une fonction définie sur un voisinage de $a$ sauf éventuellement en $a$.
La limite $\displaystyle\lim_{x\to a}f(x)$ existe si et seulement si les deux limites de $f$ à gauche de $a$ et à droite de $a$ existent et sont égales.
Exemple 1 :
Soit $f_1$ la fonction définie sur $\mathbb{R}^*$ par :
$$f_1(x)=\frac{1}{x}$$
On a $\displaystyle\lim_{ \substack{x\to 0 \\ x<0}}f(x)=-\infty$ et $\displaystyle\lim_{ \substack{x\to 0 \\ x>0}}f(x)=+\infty$.
Donc,
$$\lim_{ \substack{x\to 0 \\ x<0}}f(x)\neq\lim_{ \substack{x\to 0 \\ x>0}}f(x)$$
Par conséquent, la limite $\displaystyle\lim_{x\to 0}f(x)$ n’existe pas.
Exemple 2 :
Soit $f_2$ la fonction définie sur $\mathbb{R}^*$ par :
$$f_2(x)=\frac{1}{x^2}$$
On a $\displaystyle\lim_{\substack{x\to 0 \\ x<0}}f(x)=+\infty$ et $\displaystyle\lim_{\substack{x\to 0 \\ x>0}}f(x)=+\infty$.
Donc,
$$\lim_{\substack{x\to 0 \\ x<0}}f(x)=\lim_{\substack{x\to 0 \\ x>0}}f(x)$$
Par conséquent, la limite $\displaystyle\lim_{x\to 0}f(x)$ existe et égale à $+\infty$.
FIN
Je suis ingénieur télécoms de formation et j’exerce ce métier depuis toujours. Je reste cependant passionné par les mathématiques et très proche de ce domaine.
À travers mathsland, je m’enrichis chaque jour au contact de personnes remarquables, passionnées et passionnantes.