Soit $f$ la fonction définie sur $\mathbb{R}$ par :

$$f(x)=\begin{cases}\frac{x}{e^{x}-1} \,\,\,\,\,&\text{Si}\,x\neq 0\\ 1\,\qquad &\text{Si}\,x=0 \end{cases}$$

On note $C_{f}$ la courbe représentative de $f$ dans un repère orthonormal.

Préambule

1. Étudier le signe de la fonction $g$ définie par :

$$g:\,\begin{cases} \mathbb{R}\to\mathbb{R} & \\ x\mapsto (1-x)e^{x}-1& \end{cases}$$

 

2. Soient $\Delta_{1}\,$ et $\,\Delta_{2}$ les fonctions définies sur $\mathbb{R}$ par :

$\Delta_{1}(x)=e^{x}-x-1-\frac{x^{2}}{2}\,$ et $\,\Delta_{2}(x)=e^{x}-x-1-\frac{x^{2}e^{x}}{2}$

2.1 Étudier le signe de $\Delta_{1}$ et le signe de $\Delta_{2}$.

2.2 En déduire les deux encadrements suivants :

$(1)\quad$ Pour tout réel $x$ dans $]-\infty\,,\,0]$, on a : $\frac{x^{2}e^{x}}{2}\leq e^{x}-x-1\leq \frac{x^{2}}{2}$

$(2)\quad$ Pour tout réel $x$ dans $[0\,,\,+\infty[$, on a : $\frac{x^{2}}{2}\leq e^{x}-x-1\leq \frac{x^{2}e^{x}}{2}$

Partie I

L’objectif de cette partie est l’étude de la fonction $f$.

1. Montrer que $f$ est continue sur $\mathbb{R}$.

2. Montrer que $f$ est dérivable sur $\mathbb{R}$ et calculer $f'(x)$ pour tout $x\in\mathbb{R}$.

3. Montrer que quelque soit le réel $x$, on a $f'(x)<0$.

4. Déterminer les limites : $\displaystyle\lim_{x\to -\infty}f(x)$ et $\displaystyle\lim_{x\to +\infty}f(x)$ et préciser les équations des aymptotes à $C_{f}$ au voisinage de l’infini.

5. Dresser le tableau de variations de $f$.

6. Tracer l’allure de $C_{f}$. On précisera la démarche suivie pour le tracé.

 

Partie II

L’objectif de cette partie est l’étude d’une suite récurrente associée à la fonction $f$.

Soit $n$ un entier naturel.

On considère la suite $\displaystyle (u_{n})_{n\in\mathbb{N}}$ définie par $u_{0}=1$ et pour tout $n\in\mathbb{N}$ par $\displaystyle u_{n+1}=f(u_{n})$.

1. Montrer que $f$ admet un unique point fixe que l’on précisera. On note $\alpha$ ce point fixe.

2. Vérifier que pour tout réel $x$ appartenant à l’intervalle $[0\,,\,+\infty[$, on a :

$$e^{2x}-2xe^{x}-1\geq 0$$

3. Montrer que pour tout réel $x$ strictement positif, on a :

$$f'(x)+\frac{1}{2}=\frac{e^{2x}-2xe^{x}-1}{2(e^{x}-1)^{2}}$$

4. Montrer que pour tout réel $x$ appartenant à l’intervalle $[0\,,\,+\infty[$, on a :

$$-\frac{1}{2}\leq f'(x)<0$$

5. Établir que pour tout entier naturel $n$, on a :

$$|u_{n+1}-\alpha|\leq\frac{1}{2}\,|u_{n}-\alpha|$$

6. En déduire que pour tout entier naturel $n$, on a :

$$|u_{n}-\alpha|\leq\frac{1}{2^{n}}\,(1-\alpha)$$

7. Conclure quant à la convergence de la suite $(u_{n})_{n\in\mathbb{n}}$.

 

Partie III

L’objectif de cette partie est l’étude d’une fonction définie par une intégrale.

Soit $G$ la fonction définie par :

$$G:\,\begin{cases} \mathbb{R}\to\mathbb{R} & \\ x\mapsto\int_{x}^{2x}f(t)dt& \end{cases}$$

1. Montrer que $G$ est dérivable sur $\mathbb{R}$ et que, pour tout réel $x$, on a :

$$G'(x)=\begin{cases} \frac{x(3-e^{x})}{e^{2x}-1} \qquad\text{Si}\,x\neq 0\\ 1\qquad\qquad\,\, \text{Si}\,x=0 \end{cases}$$

2. Montrer que pour tout réel $x$ appartenant à l’intervalle $[0\,,\,+\infty[$, on a :

$$0\leq G(x)\leq xf(x)$$

En déduire la limite : $\displaystyle\lim_{x\to +\infty}G(x)$

3. Montrer que tout réel $x$ appartenant à l’intervalle $]-\infty \,,\,0]$, on a :

$$G(x)\leq xf(x)$$

En déduire la limite : $\displaystyle\lim_{x\to -\infty}G(x)$

4. Dresser le tableau de variations de $G$.

FIN

Vous trouverez dans cet onglet des indications pour les question délicates ou particulièrement difficiles

Partie II – Question 4

Utiliser l’égalité établie à la question 3 de la même partie en faisant attention que cette égalité n’est pas valable en $0$. Il faut donc traiter le cas $x=0$ séparément.

Partie II – Question 5

Utiliser l’inégalité des accroissements finis et prendre soin de vérifier toutes les conditions de son application.

Préambule

1. Étude du signe de la fonction $g$ définie par :

$$g:\,\begin{cases} \mathbb{R}\to\mathbb{R} & \\ x\mapsto (1-x)e^{x}-1& \end{cases}$$

La connaissance des variations de $g$ permet de répondre à cette question, et on a :

Les fonctions $x\mapsto 1-x$ et $x\mapsto e^{x}$ sont dérivables sur $\mathbb{R}$, donc par produit, la fonction $x\mapsto (1-x)e^{x}$ est dérivable sur $\mathbb{R}$ puis par somme, $g$ est dérivable sur $\mathbb{R}$ et pour tout $x\in\mathbb{R}$, on a :

$$\begin{align} g’(x)&=-e^{x}+(1-x)e^{x}\\&=e^{x}(-1+1-x)\\&=-xe^{x} \end{align}$$

Tableau de variation de $g$ :

$$\large\begin{array}{|c|lcccr|} \hline x & -\infty\qquad&&\qquad 0 \qquad &&\qquad +\infty \\  \hline \text{Signe de } g’ & &+&&- &\\ \hline \hline\\ \text{Variations de } g &&\nearrow&0&\searrow &\\ \\ \hline \end{array}$$

Donc d’après le tableau de variations ci-dessus, on a : $\forall x\in\mathbb{R}\,,\,g(x)\leq 0$.

2.1 Étude du signe de $\Delta_{1}$ et du signe de $\Delta_{2}$ :

Signe de $\Delta_{1}$ :

$\Delta_{1}$ est définie sur $\mathbb{R}\,$ par $\Delta_{1}(x)=e^{x}-x-1-\frac{x^{2}}{2}$.

$\Delta_{1}$ est la somme des fonctions $x\mapsto e^{x}$ et $x\mapsto -x-1-\frac{x^{2}}{2}$.

La fonction $x\mapsto -x-1-\frac{x^{2}}{2}$ est une fonction polynomiale donc dérivable sur $\mathbb{R}$. La fonction $x\mapsto e^{x}$ est dérivable sur $\mathbb{R}$. Donc par somme, $\Delta_{1}$ est dérivable sur $\mathbb{R}$ et on a :

$$\forall x\in\mathbb{R}\,,\qquad\Delta_{1}'(x)=e^{x}-1-x$$

L’expression de $\Delta_{1}’$ ainsi obtenue ne permet de déterminer directement son signe.

Calculons $\Delta_{1}^{\prime\prime}$ :

$\Delta_{1}’$ est dérivable sur $\mathbb{R}$ comme somme de fonctions dérivables sur $\mathbb{R}$ et on a :

$$\forall x\in\mathbb{R}\,,\qquad\Delta_{1}^{\prime\prime}(x)=e^{x}-1$$

Tableau de signe de $\Delta_{1}$ :
$$\large\begin{array}{|c|ccccc|}\hline x&-\infty&\qquad\qquad&&0&&\qquad\qquad&+\infty \\ \hline \text{Signe de } \Delta_{1}^{\prime\prime}(x)&&-&&0&&+& \\ \hline \text{Variations de } \Delta_{1}’&&\searrow&&0&&\nearrow& \\ \hline \text{Signe de } \Delta_{1}’(x)&&+&&0&&+&\\ \hline \text{Variations de } \Delta_{1}&&\nearrow&&0&&\nearrow& \\\hline\text{Signe de }\Delta_{1}&&-&&0&&+&\\\hline\end{array}$$

 

$\Delta_{1}$ est négative sur $]-\infty\,,\,0]$ et positive sur $[0\,,\,+\infty[$.

Signe de $\Delta_{2}$ :

$\Delta_{2}$ est définie sur $\mathbb{R}$ par $\Delta_{2}(x)=e^{x}-x-1-\frac{x^{2}e^{x}}{2}$.

La fonction $\Delta_{2}$ est la somme des fonctions $x\mapsto e^{x}$, $x\mapsto -x-1$ et $x\mapsto -\frac{x^{2}e^{x}}{2}$.

La fonction $x\mapsto e^{x}$ est dérivable sur $\mathbb{R}$, et la fonction $x\mapsto -x-1$ est une fonction affine (donc polynomiale) donc dérivable sur $\mathbb{R}$.

la fonction $x\mapsto -\frac{x^{2}e^{x}}{2}$ est le produit des fonctions $x\mapsto -\frac{x^{2}}{2}$ dérivable sur $\mathbb{R}$ et de $x\mapsto e^{x}$ dérivable sur $\mathbb{R}$. Par produit, $x\mapsto -\frac{x^{2}e^{x}}{2}$ est dérivable sur $\mathbb{R}$, puis par somme, $\Delta_{2}$ est dérivable sur $\mathbb{R}$ et on a :

$$\forall x\in\mathbb{R}\,,\qquad\Delta_{2}^{\prime}(x)=e^{x}-1-xe^{x}-\frac{x^{2}e^{x}}{2}$$

L’expression de $\Delta_{2}’$ ainsi obtenue ne permet de déterminer directement son signe.

Calculons $\Delta_{2}^{\prime\prime}$ :

$\Delta_{2}’$ est dérivable sur $\mathbb{R}$ par produit et somme de fonctions dérivables sur $\mathbb{R}$ et on a pour tout réel $x$ :

$$\begin{align}\Delta_{2}^{\prime\prime}(x)&=e^{x}-(e^{x}+xe^{x})-(xe^{x}+\frac{x^{2}e^{x}}{2})\\&=\frac{x^{2}e^{x}}{2}\end{align}$$

Tableau de signe de $\Delta_{2}$ :

$$\begin{array}{|c|ccccc|}\hline x&-\infty&\qquad\qquad&&0&&\qquad\qquad&+\infty \\ \hline \text{Signe de } \Delta_{2}^{\prime\prime}(x)&&+&&0&&+& \\ \hline \text{Variations de } \Delta_{2}’&&\nearrow&&0&&\nearrow& \\ \hline \text{Signe de } \Delta_{2}’(x)&&-&&0&&-&\\ \hline \text{Variations de } \Delta_{2}&&\searrow&&0&&\searrow&\\ \hline \text{Signe de }\Delta_{2}&&+&&0&&-&\\\hline\end{array}$$

 

$\Delta_{2}$ est positive sur $]-\infty\,,\,0]$ et négative sur $[0\,,\,+\infty[$.

2.2 Les encadrements :

D’après les deux tableaux de signes ci-dessus, on a :

• Pour tout réel $x$ dans $]-\infty\,,\,0]\,$, $\displaystyle\frac{x^{2}e^{x}}{2}\leq e^{x}-x-1\leq\frac{x^{2}}{2}$

• Pour tout réel $x$ dans $[0\,,\,+\infty[\,$, $\displaystyle\frac{x^{2}}{2}\leq e^{x}-x-1\leq\frac{x^{2}e^{x}}{2}$

Partie I

L’objectif de cette partie est l’étude de la fonction $f$ définie sur $\mathbb{R}$ par :

$$f(x)=\begin{cases}\frac{x}{e^{x}-1} \,\,\,\,\,&\text{Si}\,x\neq 0\\ 1\,\qquad &\text{Si}\,x=0 \end{cases}$$

Et de tracer l’allure de sa courbe représentative $C_{f}$ dans un repère orthonormal.

 

1. Continuité de $f$ :

Il s’agit de montrer que $f$ est continue sur $\mathbb{R}$.

Pour $x\neq 0$ :

$f$ est le quotient de $x\mapsto x$ par $x\mapsto e^{x}-1$. Or la fonction $x\mapsto x$ est continue sur $\mathbb{R}$ et la fonction $x\mapsto e^{x}-1$ est continue et ne s’annule pas sur $\mathbb{R^{*}}$, donc par quotient, $f$ est continue sur $\mathbb{R^{*}}$.

Continuité en zéro :

$f$ est continue en zéro si et seulement si, $\displaystyle\lim_{x\to 0}f(x)=f(0)$.

On a,

$$\begin{align} \lim_{x\to 0}f(x)&=\lim_{x\to 0}\frac{x}{e^{x}-1}\\&=\lim_{x\to 0}\left(\frac{1}{\frac{e^{x}-1}{x}}\right)\end{align}$$

On remarque que pour $x\neq 0$, $\displaystyle\frac{e^{x}-1}{x}=\frac{h(x)-h(0)}{x-0}$ où $h(x)=e^{x}$.

On sait par ailleurs que $h$ est dérivable en $0$, donc le taux d’accroissement $\displaystyle\frac{h(x)-h(0)}{x-0}$ admet une limite finie en $0$ et on a $\displaystyle\lim_{x\to 0}\frac{h(x)-h(0)}{x-0}=h'(0)=1$.

D’où, $$\begin{align}\lim_{x\to 0}f(x)&=\lim_{x\to 0}\left(\frac{1}{\frac{e^{x}-1}{x}}\right)\\&=\frac{1}{1}\\&=f(0)\end{align}$$

$f$ est continue sur $\mathbb{R^{*}}$ et en $0$. $f$ est donc continue sur $\mathbb{R}$.

 

2. Dérivabilité de $f$ et expression de $f’$ :

Pour $x\neq 0$, $\displaystyle f(x)=\frac{x}{e^{x}-1}$.

$f$ est le quotient de $x\mapsto x$ par $x\mapsto e^{x}-1$. Or la fonction $x\mapsto x$ est dérivable sur $\mathbb{R}$ et la fonction $x\mapsto e^{x}-1$ est dérivable et ne s’annule pas sur $\mathbb{R^{*}}$, donc par quotient, $f$ est dérivable sur $\mathbb{R^{*}}$.

 

Pour $x=0$ :

$f$ est dérivable en $0$ si et seulement si le taux d’accroissement $\displaystyle\frac{f(x)-f(0)}{x}$ admet une limite finie lorsque $x$ tend vers $0$.

Pour $x\neq 0$, on a :

$$\begin{align}\frac{f(x)-f(0)}{x}&=\frac{\frac{x}{e^{x}-1}-1}{x}\\&=\frac{x+1-e^{x}}{x(e^{x}-1)}\\&=\frac{x+1-e^{x}}{x^{2}}\times\frac{x}{e^{x}-1}\end{align}$$

Soit par passage à la limite,

$$\lim_{x\to 0}\frac{f(x)-f(0)}{x}=\lim_{x\to 0}\left(\frac{x+1-e^{x}}{x^{2}}\times\frac{x}{e^{x}-1}\right)$$

On a d’une part,

$\displaystyle\lim_{x\to 0}\frac{x}{e^{x}-1}=f(0)=1$ car $f$ est continue en $0$.

Et d’autre part, d’après les encadrements démontrés au préambule :

Pour $x<0$, on a :

$$\displaystyle\frac{x^{2}e^{x}}{2} < e^{x}-x-1 <\frac{x^{2}}{2}$$

Soit en multipliant par $-1$ pour faire apparaître l’expression recherchée :

$$-\frac{x^{2}}{2} < x+1-e^{x} < -\frac{x^{2}e^{x}}{2}$$

Puis en divisant par $x^{2}$ qui est strictement positif,

$$ -\frac{1}{2} < \frac{x+1-e^{x}}{x^{2}} < -\frac{e^{x}}{2}$$

Comme $\displaystyle\lim_{\substack{x\to 0 \\ x<0}}\frac{e^{x}}{2}=-\frac{1}{2}$ alros $\displaystyle\lim_{\substack{x\to 0 \\ x<0}}\frac{x+1-e^{x}}{x^{2}}=-\frac{1}{2}$ d’après le théorème des gendarmes.

 

Pour $x>0$, on a :

$$\frac{x^{2}}{2}\leq e^{x}-x-1\leq\frac{x^{2}e^{x}}{2}$$

Soit en multipliant par $-1$ :

$$ -\frac{x^{2}e^{x}}{2}\leq x+1-e^{x}\leq -\frac{x^{2}}{2}$$

Puis en divisant par $x^{2}$ qui est strictement positif,

$$-\frac{e^{x}}{2}\leq \frac{x+1-e^{x}}{x^{2}}\leq -\frac{1}{2}$$

Puis conclure à l’aide du théorème des gendarmes que :

$$\lim_{\substack{x\to 0 \\ x>0}}\frac{x+1-e^{x}}{x^{2}}=-\frac{1}{2}$$

 

On a donc  $\displaystyle\lim_{\substack{x\to 0 \\ x<0}}\frac{x+1-e^{x}}{x^{2}}=\lim_{\substack{x\to 0 \\ x>0}}\frac{x+1-e^{x}}{x^{2}}=-\frac{1}{2}$ donc $\displaystyle\lim_{x\to}\frac{x+1-e^{x}}{x^{2}}=-\frac{1}{2}$.

$f$ est donc dérivable en $0$ et $\displaystyle f'(0)=-\frac{1}{2}$.

$f$ est dérivable sur $\mathbb{R^{*}}$ et en $0$. $f$ est donc dérivable sur $\mathbb{R}$.

Expression de la dérivée $f’$ :

$f$ est dérivable sur $\mathbb{R}$ et pour tout réel $x$, on a :

$$\begin{align} f’(x)&=\frac{1(e^{x}-1)-xe^{x}}{(e^{x}-1)^{2}}\\&=\frac{(1-x)e^{x}-1}{(e^{x}-1)^{2}}\end{align}$$

 

$f$ est dérivable sur $\mathbb{R}$ et pour tout réel $x$, $\displaystyle f'(x)=\frac{(1-x)e^{x}-1}{(e^{x}-1)^{2}}$.

En particulier, $f'(0)=-\frac{1}{2}$

 

3. Signe de $f'(x)$ :

Il s’agit ici de démontrer que pour tout $x\in\mathbb{R}$, $f'(x)<0$.

Il faut distinguer deux cas car l’expression de $f’$ diffère selon que $x\neq 0$ (1er cas) ou $x=0$ (2ème cas).

Pour $x\neq 0$, on a démontré à la question précédente que $f'(x)=\frac{(1-x)e^{x}-1}{(e^{x}-1)^{2}}=\frac{g(x)}{(e^{x}-1)^{2}}$ où $g$ est la fonction étudiée en préambule.

Comme $g$ est strictement négative sur $\mathbb{R^{*}}$, alors $f'(x)<0$ pour tout $x\in\mathbb{R^{*}}$.

 

Pour $x=0$, on a $f'(0)=-\frac{1}{2}<0$.

Finalement, pour tout $x\in\mathbb{R}$, on a $f'(x)<0$.

 

4. Limites et comportement asymptotique de $f$ :

Calcul de la limite $\displaystyle\lim_{x\to +\infty}f(x)$ :

On a,

$$\begin{align}\lim_{x\to +\infty}f(x)&=\lim_{x\to +\infty}\frac{x}{e^{x}-1}\\&=\lim_{x\to +\infty}\frac{x}{e^{x}(1-e^{-x})}\\&=\lim_{x\to +\infty}\bigg(\frac{x}{e^{x}}\times\frac{1}{1-e^{-x}}\bigg)\end{align}$$

Or $\displaystyle\lim_{x\to +\infty}\frac{x}{e^{x}}=0$ d’après le théorème des croissances comparées, d’une part, et d’autre part, $\displaystyle\lim_{x\to +\infty}\frac{1}{1-e^{-x}}=1$, donc,

$$\lim_{x\to +\infty}f(x)=0$$

On en déduit que l’axe des abscisses ($y=0$) est asymptote à la courbe $C_{f}$ au voisinage de $+\infty$.

 

Calcul de la limite $\displaystyle\lim_{x\to -\infty}f(x)$ :

On a $\displaystyle\lim_{x\to -\infty}f(x)=\lim_{x\to -\infty}\frac{x}{e^{x}-1}$.

Or, $\displaystyle\lim_{x\to -\infty}x=-\infty$ et $\displaystyle\lim_{x\to -\infty}e^{x}-1=-1$, donc par quotient, on a :

$$\displaystyle\lim_{x\to -\infty}f(x)=\lim_{x\to -\infty}\frac{x}{e^{x}-1}=+\infty$$

 

Recherche des branches infinies :

Connaissant le comportement de $C_{f}$ au voisinage de $+\infty$ ($C_{f}$ admet l’axe des abscisses comme asymptote (horizontale) au voisinage de $+\infty$), nous allons donc nous intéresser au comportement de $f$ au voisinage de $-\infty$.

Pour tout $\displaystyle x\neq 0$, on a $\frac{f(x)}{x}=\frac{1}{e^{x}-1}$, donc $\displaystyle\lim_{x\to -\infty}\frac{f(x)}{x}=\lim_{x\to -\infty}\frac{1}{e^{x}-1}=-1$, d’une part.

Et d’autre part, on a :

$$\begin{align}f(x)+x&=\frac{x}{e^{x}-1}+x\\&=\frac{x+xe^{x}-x}{e^{x}-1}\\&=\frac{xe^{x}}{e^{x}-1}\end{align}$$

Par passage à la limite, on a :

$$\begin{align}\lim_{x\to -\infty}(f(x)+x)&=\lim_{x\to -\infty}\frac{xe^{x}}{e^{x}-1}\end{align}$$

Or $\displaystyle\lim_{x\to -\infty}xe^{x}=0$, d’après le théorème des croissances comparées, et $\displaystyle\lim_{x\to -\infty}e^{x}-1=-1$, donc par quotient, on a $\displaystyle\lim_{x\to -\infty} (f(x)+x)=0$.

La courbe $C_{f}$ admet deux asymptotes. 1/ L’axe des abscisses ($y=0$) comme asymptote horizontale au voisinage de $+\infty$, et 2/ La droite d’équation $y=-x$ comme asymptote (oblique) au voisinage de $-\infty$.

 

5. Tableau de variations de $f$ :

Puisque $f’$ est strictement négative sur $\mathbb{R}$ (question 3), alors $f$ est strictement décroissante sur $\mathbb{R}$.

Tableau de variations de $f$ :

$$\large\begin{array}{|c|lcccr|} \hline x & -\infty\qquad&&\qquad 0 \qquad &&\qquad +\infty \\  \hline \text{Signe de } f’ & &-&-\frac{1}{2}&- &\\ \hline \hline\\ \text{Variations de } f &+\infty&\searrow&1&\searrow &0\\ \\ \hline \end{array}$$

 

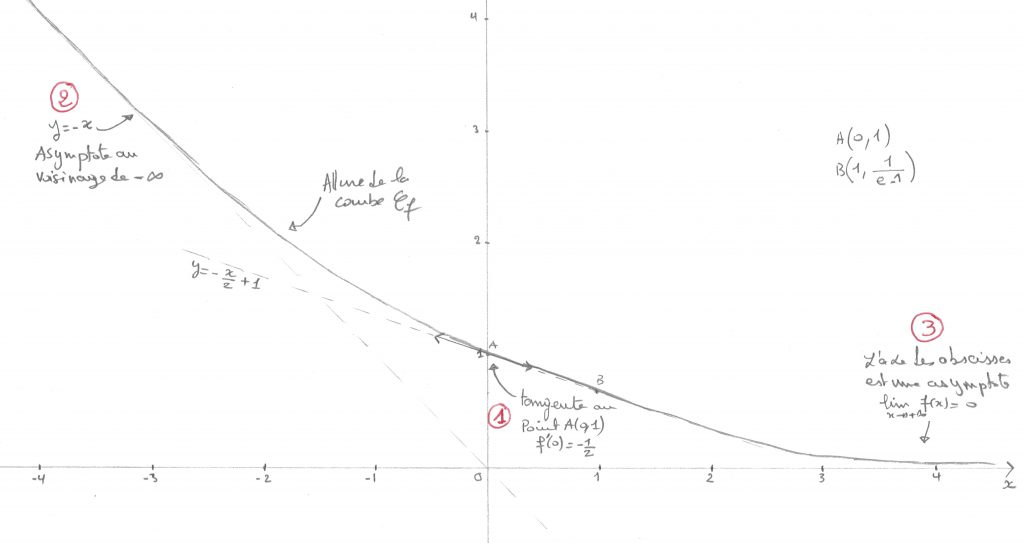
6. Allure de la courbe $C_{f}$ :

On sait d’après les questions précédentes que :

• La droite d’équation $y=-x$ est asymptote à la courbe $C_{f}$ au voisinage de $-\infty$.
• L’axe des abscisses est asymptote à la courbe $C_{f}$ au voisinage de $+\infty$.
• $f'(0)=-\frac{1}{2}$\,, qui est le coefficient directeur de la tangente à $C_{f}$ au point $(0,f(0))$. Une équation de cette tangente est : $y=-\frac{x}{2}+1$.
• $f$ est décroissante.

À la lumière de ces renseignements sur $f$, on peut tracer l’allure de la courbe $C_{f}$ à la main :

 

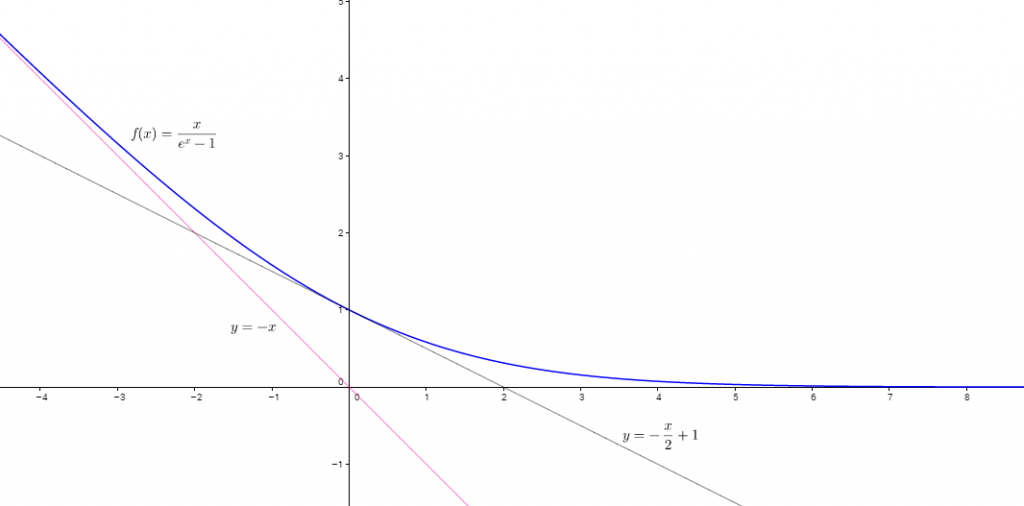
Allure de la courbe $C_{f}$ avec le logiciel Geogerba :

 

 

Partie II

L’objectif de cette partie est l’étude de la suite $(u_{n})_{n\in{\mathbb{N}}}$ associée à la fonction $f$.

$n$ est un entier naturel.

On considère la suite $\displaystyle (u_{n})_{n\in\mathbb{N}}$ définie par $u_{0}=1$ et pour tout $n\in\mathbb{N}$ par $\displaystyle u_{n+1}=f(u_{n})$.

1. Montrer que $f$ admet un unique point fixe noté $\alpha$ :

L’expression de $f$ change selon que $x$ est égal à $0$ ou $x$ est différent de $0$. Il faut donc prendre ces deux cas en considération.

Si $x=0$, on a $f(0)=1$. Zéro n’est donc pas un point fixe pour $f$ (car $f(0)\neq 0$).

 

Soit $x$ un réel différent de zéro.

On a $f(x)=\frac{x}{e^{x}-1}$.

Montrer que $f$ admet un unique point fixe revient à montrer que l’équation $f(x)=x$ admet une unique solution.

$$\begin{align}\forall x\neq 0\,,\qquad f(x)=x&\Longleftrightarrow \frac{x}{e^{x}-1}=x\\&\Longleftrightarrow\frac{x}{e^{x}-1}=1\\&\Longleftrightarrow e^{x}-1=1\\&\Longleftrightarrow e^{x}=2\\&\Longleftrightarrow x=\ln(2)\end{align}$$

 

$f$ admet un unique point fixe $\alpha=\ln(2)$.

 

2. Vérifier que pour tout réel $x\in [0\,,\,+\infty[$, on a $e^{2x}-2xe^{x}-1\geq 0$ :

On pose, pour $x$ dans $[0\,,\,+\infty[$ :

$$u(x)=e^{2x}-2xe^{x}-1$$

L’inégalité proposée s’écrit :

$$\forall x\in [0\,,\,+\infty[\,,\,u(x)\geq 0$$

Il s’agit donc de déterminer le signe de $u$. La connaissance des variations de $u$ pourrait permettre de répondre à cette question. On a :

La fonction $x\mapsto e^{2x}$ est dérivable sur $[0\,,\,+\infty[$ par composition des deux fonctions $x\mapsto 2x$ et $x\mapsto e^{x}$ toutes deux dérivables sur $[0\,,\,+\infty[$.

La fonction $x\mapsto 2xe^{x}$ est dérivable sur $[0\,,\,+\infty[$ par produit des deux fonctions $x\mapsto 2x$ et $x\mapsto e^{x}$ toutes deux dérivables sur $[0\,,\,+\infty[$.

Donc $u$ est dérivable sur $[0\,,\,+\infty[$ comme somme de fonctions dérivables sur $[0\,,\,+\infty[$.

$$\begin{align}\forall x\in [0\,,\,+\infty[\,,\qquad u'(x)&=2e^{2x}-2(e^{x}+xe^{x})\\&=2e^{2x}-2(1+x)e^{x}\\&=2e^{x}(e^{x}-x-1)\end{align}$$

L’expression de $u'(x)$ ainsi obtenue ne permet pas de conclure quant au signe de $u’$. Introduisons la fonction $v$ définie sur $[0\,,\,+\infty[$ par $v(x)=e^{x}-x-1$ et étudions son signe.

$v$ est dérivable sur $[0\,,\,+\infty[$ comme somme de fonctions dérivables sur $[0\,,\,+\infty[$ et pour tout réel $x$ appartenant à l’intervalle $[0\,,\,+\infty[$, on a : $v'(x)=e^{x}-1$.

 

Tableau de signe de $u$ :

 

$$\large\begin{array}{|c|lcr|} \hline x & 0\qquad\qquad\qquad & & \qquad\qquad\qquad+\infty \\  \hline \text{Signe de } v’(x) & & + &  \\ \hline \text{Variations de } v(x) &0& \nearrow & \\ \hline \text{Signe de } u’(x) & & + &\\  \hline \\  \text{Variations de } u &0 & \nearrow & \\  \\ \hline \end{array}$$

 

Pour tout réel $x$ de $[0\,,\,+\infty[$, on a $e^{2x}-2xe^{x}-1\geq 0$.

 

3. Montrer que pour tout réel $x$ strictement positif, on a :

$$f'(x)+\frac{1}{2}=\frac{e^{2x}-2xe^{x}-1}{2(e^{x}-1)^{2}}$$

Soit $x>0$, on a :

$$\begin{align}f'(x)+\frac{1}{2}&=\frac{(1-x)e^{x}-1}{(e^{x}-1)^{2}}+\frac{1}{2}\\&=\frac{2(1-x)e^{x}-2+(e^{x}-1)^{2}}{2(e^{x}-1)^{2}}\\&=\frac{2e^{x}-2xe^{x}-2+e^{2x}-2e^{x}+1}{2(e^{x}-1)^{2}}\\&=\frac{e^{2x}-2xe^{x}-1}{2(e^{x}-1)^{2}}\end{align}$$

 

Pour tout réel $x$ strictement positif, on a $\displaystyle f'(x)+\frac{1}{2}=\frac{e^{2x}-2xe^{x}-1}{(e^{x}-1)^{2}}$.

 

4. Encadrement de $f'(x)$ :

On se propose dans cette question de démontrer que pour tout réel $x$ supérieur ou égal à zéro, on a $-\frac{1}{2}\leq f'(x)<0$.

L’inégalité de droite, c’est à dire que $\forall x\in [0\,,\,+\infty[$, $f'(x)<0$, a été démontrée à la question 3 de la partie I (valable sur tout $\mathbb{R}$). Il reste à démontrer l’inégalité de gauche, c’est à dire que $\forall x\in [0\,,\,+\infty[$, $-\frac{1}{2}\leq f'(x)$

On a démontré à la question précédente que pour tout réel $x$ strictement positif, on a : $\displaystyle f'(x)+\frac{1}{2}=\frac{e^{2x}-2xe^{x}-1}{(e^{x}-1)^{2}}$.

À la question 2/Partie II, on a établit que pour tout réel $x$ dans $[0\,,\,+\infty[$, on a $e^{2x}-2xe^{x}-1\geq 0$. On en déduit que :

$$\forall x\in ]0\,,\,+\infty[\,,\,f'(x)+\frac{1}{2}\geq 0$$

Notons ici que l’intervalle est ouvert sur zéro. Cela provient du fait que l’égalité $\displaystyle f'(x)+\frac{1}{2}=\frac{e^{2x}-2xe^{x}-1}{(e^{x}-1)^{2}}$ est valable pour $x$ strictement positif.

C’est à dire,

$$\forall x\in ]0\,,\,+\infty[\,,\,f'(x)\geq -\frac{1}{2}$$

Ou encore,

$$\forall x\in ]0\,,\,+\infty[\,,\,-\frac{1}{2}\leq f'(x)$$

 

Enfin, comme $\displaystyle f'(0)=-\frac{1}{2}$ , alors $\displaystyle\forall x\in [0\,,\,+\infty[\,,\,-\frac{1}{2}\leq f'(x)$.

 

On en déduit que, $\forall x\in [0\,,\,+\infty [$, on a $\displaystyle -\frac{1}{2}\leq f'(x)<0$.

5. Établir que pour tout entier naturel $n$, on a :

$$|u_{n+1}-\alpha|\leq\frac{1}{2}|u_{n}-\alpha|$$

L’inégalité à démontrer suggère l’utilisation de l’inégalité des accroissements finis. Cependant, il ne faut pas oublier de vérifier avec soin les conditions de son application

On se place dans l’intervalle $I=[0\,,\,+\infty[$ et on justifie/démontre les points suivants :

• $f$ est continue sur $I$ et dérivable sur $]0\,,\,+\infty[$,
• $f’$ est bornée sur $]0\,,\,+\infty[$,
• $f(I)\subset I$,
• $u_{0}\in I$,
• la suite $(u_{n})$ est définie,
• $u_{n}\in I$ pour tout entier naturel $n$,
• $\alpha\in I$.

$f$ est continue sur $I$ (Question 1) et dérivable sur $]0\,,\,+\infty[$ (Question 2).

On a montré à la question précédente que $f’$ est donc strictement négative ($\forall x\in I$ , $\displaystyle -\frac{1}{2}\leq f'(x)<0$), on en déduit que : $\displaystyle\forall x\in I$  , $\displaystyle |f'(x)|=-f'(x)\leq\frac{1}{2}$ et $\frac{1}{2}\in I$.

Par ailleurs, $f$ est continue et décroissante sur $I$ avec $f(0)=1$ et $\displaystyle\lim_{x\to +\infty}f(x)=0$. Donc $f(I)=[1\,,\,0[\subset I$. Notons au passage que $I$ est stable par $f$. Cette condition est importante pour la définition de la suite $(u_{n})$.

$u_{0}\in I$ :

C’est une donnée de l’énoncé. ($u_{0}=1\in I$).

La suite $\displaystyle (u_{n})_{n\in\mathbb{N}}$ est définie par $u_{0}=1$ et pour tout $n\in\mathbb{N}$ par $\displaystyle u_{n+1}=f(u_{n})=\frac{u_{n}}{e^{u_{n}}-1}$.

Pour montrer que la suite $(u_{n})_{n\in\mathbb{N}}$ est bien définie, il faut et il suffit de montrer que $e^{u_{n}}-1\neq 0$, soit $u_{n}\neq 0$.

De par sa définition, on a $\displaystyle u_{n}=f(u_{n-1})$, or $\forall x\mathbb{R}$ , $f(x)>0$, donc $\displaystyle u_{n}=f(u_{n-1})>0$.

La suite $\displaystyle (u_{n})_{n\in\mathbb{N}}$ est bien définie et à valeurs dans $]0\,,\,+\infty[$.

Remarque :

Si nous ne connaissions pas le signe de $f$, alors il aura fallu montrer par récurrence que la suite $\displaystyle (u_{n})_{n\in\mathbb{N}}$ est bien définie et à valeurs dans $]0\,,\,+\infty[$.

 

$\alpha\in I$ :

On sait que $\alpha=\ln(2)\in I$.

Toutes les hypothèse étant vérifiées, on applique l’inégalité des accroissements finis à la fonction $f$ entre $u_{n}$ et $\alpha$ et on obtient :

$$f(u_{n})-f(\alpha)|\leq\frac{1}{2}|u_{n}-\alpha|$$

Soit avec $f(u_{n})=u_{n+1}$ et $f(\alpha)=\alpha$,

$$|u_{n+1}-\alpha|\leq\frac{1}{2}|u_{n}-\alpha|$$

 

Pour tout entier naturel $n$, on a $\displaystyle |u_{n+1}-\alpha|\leq\frac{1}{2}|u_{n}-\alpha|$

6. En déduire que pour tout entier naturel $n$, on a :

$$|u_{n}-\alpha|\leq\frac{1}{2^{n}}(u_{0}-\alpha)$$

On démontre cette inégalité par récurrence.

pour $n\in\mathbb{N}$, on note $\mathcal{P_{n}}$ la propriété :

$$|u_{n}-\alpha|\leq\frac{1}{2^{n}}(u_{0}-\alpha)$$

Initialisation :

Pour $n=0$, on a :

$$\begin{align}|u_{0}-\alpha|&=|1-\ln(2)|\\&=\big(1-\ln(2)\big)\qquad\text{car }1\geq\ln(2)\\&=\frac{1}{2^{0}}\big(1-\alpha\big)\end{align}$$

L’inégalité est donc vraie au rang zéro.

 

Hérédité :

Fixons $n$ dans $\mathbb{N}$ tel que $\mathcal{P_{n}}$ soit vraie, on a donc :

$$|u_{n}-\alpha|\leq\frac{1}{2^{n}}(1-\alpha)$$

Pour tout entier naturel $n$, on a :

$$\begin{align}|u_{n+1}-\alpha|&\leq\frac{1}{2}|u_{n}-\alpha|\qquad\qquad\qquad\text{d’après la question 5}\\&\leq\frac{1}{2}\times\frac{1}{2^{n}}(1-\alpha)\qquad\qquad\text{d’après l’hypothèse de récurrence}\\&\leq\frac{1}{2^{n+1}}(1-\alpha)\end{align}$$

L’inégalité est vraie au rang $n+1$. Elle est donc vraie pour tout $n$.

Pour tout entier naturel $n$, on a $\displaystyle |u_{n}-\alpha|\leq\frac{1}{2^{n}}(1-\alpha)$

 

7. Convergence de la suite $(u_{n})_{n\in\mathbb{N}}$ :

On a démontré à la question précédente que pour tout entier naturel $n$,

$$|u_{n}-\alpha|\leq\frac{1}{2^{n}}(1-\alpha)$$

Que l’on peut écrire,

$$0\leq |u_{n}-\alpha|\leq\frac{1}{2^{n}}(1-\alpha)$$

Comme $\displaystyle\lim_{n\to +\infty}\frac{1}{2^{n}}=0$ (car $\frac{1}{2}<1$), alors $displaystyle\lim_{n\to +\infty}\frac{1}{2^{n}}(1-\alpha)=0$.

Alors, $\displaystyle\lim_{n\to +\infty}|u_{n}-\alpha|$ d’après le théorème des gendarme.

 

La suite $(u_{n})_{n\in\mathbb{N}}$ est convergente et sa limite vaut $\alpha=\ln(2)$.

 

Partie III

L’objectif de cette partie est l’étude de la fonction $G$ définie par :

$$G:\,\begin{cases} \mathbb{R}\to\mathbb{R} & \\ x\mapsto\int_{x}^{2x}f(t)dt& \end{cases}$$

1. $G$ est dérivable sur $\mathbb{R}$ et expression de $G'(x)$ :

$f$ est continue sur $\mathbb{R}$ (question 1/Partie I), elle y admet donc une primitive que l’on note $F$. Et on a :

$$G(x)=F(2x)-F(x)$$

Comme $F$ est dérivable sur $\mathbb{R}$, et en particulier la fonction $x\mapsto F(2x)$ est dérivable sur $\mathbb{R}$ comme composée de $x\mapsto 2x$ par $x\mapsto F(x)$, toutes deux dérivables sur $\mathbb{R}$, alors $G$ est dérivable sur $\mathbb{R}$ et on a :

$$\begin{align}\forall x\in\mathbb{R}\,,\qquad\qquad G'(x)&=\big(F(2x)-F(x)\big)’\\&=2F'(2x)-F'(x)\\&=2f(2x)-f(x)\end{align}$$

Comme l’expression de $f$ diffère selon que $x$ soit différent de $0$ ou égal à $0$, alors il faut distinguer ces deux cas.

1er cas # $x\neq 0$ :

Si $x\neq 0$ (et $2x\neq 0$), on a :

$$\begin{align}G'(x)&=2\times\frac{2x}{e^{2x}-1}-\frac{x}{e^{x}-1}\\&=\frac{4x}{(e^{x}-1)(e^{x}+1)}-\frac{x(e^{x}+1)}{(e^{x}-1)(e^{x}+1)}\\&=\frac{4x-x(e^{x}+1)}{e^{2x}-1}\\&=\frac{3x-xe^{x}}{e^{2x}-1}\\&=\frac{x(3-e^{x})}{e^{2x}-1}\end{align}$$

2ème cas # $x=0$ :

Si $x=0$, on a $f(0)=1$ et,

$$\begin{align}G'(0)=2f(0)-f(0)\\&=f(0)\\&=1\end{align}$$

 

$G$ est dérivable sur $\mathbb{R}$ et pour tout réel $x$, on a $\displaystyle G'(x)=\begin{cases} \frac{x(3-e^{x})}{e^{2x}-1} \qquad\text{Si}\,x\neq 0\\ 1\qquad\qquad\,\, \text{Si}\,x=0 \end{cases}$

 

Remarque :

Une autre manière d’aborder/rédiger cette question est d’écrire $G(x)$ sous la forme : $\displaystyle G(x)=\int_{u(x)}^{v(x)}f(t)dt$ avec $u(x)=x$ et $v(x)=2x$, et de rappeler que $f$, $u$ et $v$ sont dérivables sur $\mathbb{R}$, que $f$ est continue sur $\mathbb{R}$ avec $u(\mathbb{R})=v(\mathbb{R})=\mathbb{R}$.

Donc $G$ est dérivable sur $\mathbb{R}$ et on a :

$$\forall x\in\mathbb{R}\,,\qquad G'(x)=v'(x)f(v(x))-u'(x)f(u(x))=2f(2x)-f(x)$$

2. Montrer que pour tout $x\in [0\,,\,+\infty[$, on a $0\leq G(x)\leq xf(x)$ :

Soient, $x$ un réel de $[0\,,\,+\infty[$, et $t$ un réel de l’intervalle $[x\,,\,2x]$. (ici, $x\leq 2x$ car $x\geq 0$).

On a, $x\leq t\leq 2x$. Comme $f$ est décroissante sur $\mathbb{R}$ (donc sur $[0\,,\,+\infty[$) alors $f(x)\geq f(t)\geq f(2x)$, soit, $f(2x)\leq f(t)\leq f(x)$ en écrivant les inégalités dans « le sens conventionnel ».

On sait par ailleurs que pour tout réel $x$, $f(x)\geq 0$, donc, $0\leq f(2x)\leq f(t)\leq f(x)$.

L’inégalité qui nous intéresse et qui va nous permettre d’aboutir à l’encadrement demandé est : $0\leq f(t)\leq f(x)$

$f$ étant continue sur $\mathbb{R}$, on peut intégrer l’inégalité et on a $\forall x\in [0\,,\,+\infty[$ et $t\in[x\,,\,2x]$, (notons au passage que l’inégalité ne change pas de sens car ici $x\leq 2x$) :

$$\begin{align}0\leq\int_{x}^{2x}f(t)dt\leq\int_{x}^{2x}f(x)dt\\0\leq G(x))dt\leq f(x)\int_{x}^{2x}dt\\0\leq G(x)t\leq (2x-x)f(x)\end{align}$$

 

Pour tout $x\in [0\,,\,+\infty[$, on a $0\leq G(x)\leq xf(x)$.

 

Calcul de la limite $\displaystyle\lim_{x\to+\infty}G(x)$ :

On vient de montrer que pour tout $x\in [0\,,\,+\infty[$, on a $0\leq G(x)\leq xf(x)$, soit en remplaçant $f$ par sa valeur, $0\leq G(x)\leq \frac{x^{2}}{e^{x}-1}\,,\,\forall x\in [0\,,\,+\infty[$.

On va démontrer que la limite $\displaystyle\lim_{x\to +\infty}\frac{x^{2}}{e^{x}-1}$ vaut $0$ et on va conclure à l’aide du théorème des gendarmes.

$forall x\geq 0$, on a :

$$\begin{align}\frac{x^{2}}{e^{x}-1}&=\frac{x^{2}}{e^{x}(1-e^{-x})}\\&=\frac{x^{2}}{e^{x}}\times\frac{1}{1-e^{-x}}\end{align}$$

Soit, par passage à la limite,

$$\lim_{x\to +\infty}\frac{x^{2}}{e^{x}-1}=\lim_{x\to +\infty}\bigg(\frac{x^{2}}{e^{x}}\times\frac{1}{1-e^{-x}}\bigg)$$

D’après le théorème des croissances comparées, on a $\displaystyle\lim_{x\to +\infty}\frac{x^{2}}{e^{x}}=0$, et d’autre part, $\displaystyle\lim_{x\to +\infty}\frac{1}{1-e^{-x}}=1$.

On en déduit que $\displaystyle\lim_{x\to +\infty}\frac{x^{2}}{e^{x}-1}=0$

 

Finalement, on a $\displaystyle\lim_{x\to +\infty}G(x)=0$ d’après le théorème des gendarmes.

 

3. Montrer que pour tout $x\in ]-\infty\,,\, 0]$, on a $G(x)\leq xf(x)$ :

Soient, $x$ un réel appartenant à $]-\infty\,,\,0]$, et $t$ un réel appartenant à l’intervalle $[2x\,,\,x]$. (ici, $2x\leq x\leq 0$ car $x\leq 0$).

On a, $2x\leq t\leq x$. Comme $f$ est décroissante sur $\mathbb{R}$ (donc sur $]-\infty\,,\,0]$), alors $f(x)\leq f(t)\leq f(2x)$, ou encore $f(t)\geq f(x)$.

$f$ étant continue sur $\mathbb{R}$, on peut intégrer l’inégalité $f(t)\geq f(x)$ et on a $\forall x\in ]-\infty\,,\,0]$ et $t\in [2x\,,\,x]$, (notons au passage que l’inégalité change de sens car ici $2x\leq x$ et les bornes de l’intégrale sont en sens décroissant) :

$$\begin{align}\int_{x}^{2x}f(t)dt &\leq\int_{x}^{2x}f(x)dt\\G(x)&\leq (2x-x)f(x)\\G(x)&\leq xf(x)\end{align}$$

 

Pour tout $x\in ]-\infty\,,\,0]$, on a G(x)\leq xf(x)$.

 

Calcul de la limite $\displaystyle\lim_{x\to -\infty}G(x)$ :

On vient de montrer que pour tout $x\in ]-\infty\,,\,0]$, on a G(x)\leq xf(x)$, soit en remplaçant $f$ par sa valeur, $0\leq G(x)\leq \frac{x^{2}}{e^{x}-1}\,,\,\forall x\in ]-\infty\,,\,0]$.

On va démontrer que la limite $\displaystyle\lim_{x\to -\infty}\frac{x^{2}}{e^{x}-1}$ est égale à $-\infty$ et on va conclure à l’aide du théorème de comparaisons des limites.

On a $\displaystyle\lim_{x\to -\infty}xf(x)=\lim_{x\to -\infty}\frac{x^{2}}{e^{x}-1}$.

Comme $displaystyle\lim_{x\to -\infty}x^{2}=+\infty$ et $\displaystyle\lim_{x\to -\infty}e^{x}-1=-1$ alors par quotient, on a $\displaystyle\lim_{x\to -\infty}xf(x)=\lim_{x\to -\infty}\frac{x^{2}}{e^{x}-1}=-\infty$.

 

Finalement, $\displaystyle\lim_{x\to -\infty}G(x)=-\infty$

 

4. Tableau de variations de $G$ :

$$\large\begin{array}{|c|cccccr|} \hline x & -\infty\qquad&0&\qquad \qquad &\ln(3)&\qquad +\infty \\  \hline \text{Signe de } x & -&0&+& &+\\ \hline \text{Signe de } (e^{2x}-1) & -&0&+& & +\\ \hline \text{Signe de } (3-e^{x}) & +&&+&0&- \\ \hline \text{Signe de } G’ & +&1&+&0&-\\\hline \hline\\ \text{Variations de } g &\nearrow&&\nearrow&&\searrow \\ \\\hline \end{array}$$

FIN

Cet onglet intitulé « Boîte noire » permet à l’auteur de rendre compte de sa démarche, d’expliquer ses motivations et de justifier ses choix rédactionnels et méthodologiques.

 

Dérivabilité de $f$ en $0$ :

La dérivabilité de $f$ en zéro est très difficile à démontrer par calcul direct si on se limite au programme des terminales.

Les questions 2.1 et 2.2 du préambule permettent de contourner cette difficulté et de démontrer que la fonction $f$ est dérivable en $0$ et de calculer la valeur de $f'(0)$.

 

Une remarque sur l’inégalité $e^{x}>x+1$ :

On s’est appuyé à la question 2 de la partie II sur la fonction $v$ définie sur $\mathbb{R}$ par $v(x)=e^{x}-x-1$ et on a montré que pour tout réel $x$, $v(x)\leq 0$, en particulier $v(0)=0$.

Donc pour $x\neq 0$, on a $e^{x}>x+1$, et puisque la fonction $\ln$ est strictement croissante sur $\mathbb{R}_{+}^{*}$, alors on peut écrire l’inégalité précédente sous la forme :

$$\forall x\in ]-1\,,\,+\infty[\,,\qquad\ln(1+x)\leq x$$

Avec égalité si et seulement si $x=0$.

En posant $y=x+1$, on obtient :

$$\forall y\in\mathbb{R}_{+}^{*}\,,\qquad\ln(y)\leq y-1$$

Avec égalité si et seulement si $y=1$.

Une interprétation géométrique de ce résultat est que la fonction $\ln$ est au-dessus de sa tangente au point d’abscisse $1$.