Enoncé
$n$ est un entier naturel et $x$ un réel supérieur ou égal à zéro.
On considère les deux suites $(u_n)$ et $(v_n)$ définies pour tout entier naturel $n$ et pour tout réel $x$ supérieur ou égal à zéro par :
$\displaystyle u_n(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}$ et $\displaystyle v_n(x)=u_n(x)+\frac{x^n}{n!}$
PARTIE I
1. Donner les valeurs de $u_n(0)$ et de $v_n(0)$.
2. Pour les valeurs $1$, $2$ et $\sqrt{2}$ de $x$, donner les valeurs approchées à $10^{-6}$ près des termes de $u_n(x)$ pour $0\leq n\leq 10$.
3. Quelle conjecture peut-on émettre sur la suite $(u_n)$ pour $x>0$? Démontrer cette conjecture.
4. Donner une condition à satisfaire pour que la suite $(v_n)$ soit strictement décroissante, éventuellement à partir d’un certain rang.
Faire un calcul pour $x=4$.
5. Démontrer qu’avec la condition établie à la question précédente, les suites $(u_n)$ et $(v_n)$ sont adjacentes. On note alors $\ell_x$ leur limite commune.
6. En examinant les termes successifs obtenus dans la question 1 pour $x=1$, conjecturer la valeur de $\ell_1$. Quelle généralisation est suggérée en examinant les valeurs de $\ell_x$ pour $x=2$ et $x=\sqrt{2}$ ?
PARTIE II
1. On pose $I_n(x)=\frac{1}{u_n(x)}$.
1.a. Calculer $I_n(x)$ pour $x=1$ et $x=2$ et $0\leq n\leq 10$.
1.b. Quelle conjecture peut-on émettre suite à l’observation des résultats obtenus ?
2. Représenter dans des repères distincts les polynômes $u_n(x)$ et $v_n(x)$ pour $1\leq n\leq 5$. Quelle conjecture est suggérée par l’examen de ces courbes ?
3. Déterminer la fonction dérivée de la fonction $u_n$ et établir une relation entre celle-ci et $u_{n-1}$.
Quelle indice supplémentaire concernant la convergence de la suite $(u_n)$ cette relation suggère-t-elle ?
PARTIE III
L’objet de cette partie est de démontrer que $\ell_1$ est irrationnel.
1. On suppose que $\displaystyle\ell_1=\frac{p}{q}$ où $p$ et $q$ sont deux entiers strictement positifs. Déterminer un encadrement de $\ell_1$ en fonction de $u_q(1)$ et de $q$.
2. Conclure.
FIN
Indications
PARTIE I
Questions 1 et 2 :
Ces deux questions ne présentent pas de difficultés particulières mis à part un effort de calcul ![]()
Question 3 :
En observant les différentes valeurs calculées dans la question 2, quelle renseignement tirez-vous sur la monotonie de la suite $(u_n)$ ?
Question 4 :
Vous pouvez commencer par exemple par écrire que la suite $(v_n)$ est décroissante si et seulement la différence entre deux termes consécutifs est strictement négative, c’est à dire que pour tout entier naturel $k$ et pour tout réel $x$ strictement positif, $v_{k+1}-v_{k}=\cdots$ doit être strictement négative …
Question 5 :
Il faudra commencer par rappeler la définition de deux suites adjacentes. La voici pour rappel :
Pour montrer que les deux suite $(u_n)$ et $(v_n)$ sont adjacentes, il faut et il suffit de montrer que :
Pour tout entier naturel $n$, $v_n\geq u_n$.
$(u_n)$ est (strictement) croissante et $(v_n)$ est (strictement) décroissante.
La limite $\displaystyle\lim_{n\to +\infty} (v_n(x)-u_n(x))=0$.
Le point 1 se déduit de la définition des deux suites. Le point 2 a été démontré dans les question 3 et 4. Il reste le point 3.
Question 6 :
À l’aide de la calculatrice, vous pouvez évaluer les valeurs de $e$, $e^2$ et de $e^{\sqrt{2}}$ puis les comparer avec les valeurs approchées de $u_n(1)$, $u_n(2)$ et $u_n(\sqrt{2})$ pour $n$ allant de $0$ à $10$ !
PARTIE II
Question 1.a :
Cette question ne présente pas difficultés particulières mis à part des efforts de calcul !
Question 1.b :
À l’aide de la calculatrice, vous pouvez évaluer les valeurs de $e^{-1}$ et $e^{-2}$ puis les comparer avec les valeurs approchées de $I_n(1)$ et $I_n(2)$ pour $n$ allant de $0$ à $10$ !
Question 2 :
Vous pouvez comparer les courbes tracées avec la courbe représentative de la fonction exponentielle ($x\mapsto e^x$) !
Question 3 :
Il s’agit de dériver une fonction polynomiale ![]()
PARTIE III
Question 1 :
Le fait que les deux suites $(u_n)$ et $(v_n)$ soient adjacentes donne une renseignement sur leur limite commune. En effet, vous avez $u_n(1) < \ell_1 < v_n(1)$ …
Question 2 :
Il faudra raisonner par l’absurde !
FIN
Corrigé
$n$ est un entier naturel et $x$ un réel supérieur ou égal à zéro.
On considère les deux suites $(u_n)$ et $(v_n)$ définies pour tout entier naturel $n$ et pour tout réel $x$ supérieur ou égal à zéro par :
$\displaystyle u_n(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}$ et $\displaystyle v_n(x)=u_n(x)+\frac{x^n}{n!}$
PARTIE I
1. Valeurs de $u_n(0)$ et de $v_n(0)$ :
Pour tout entier naturel $n$ et pour tout réel $x$ supérieur ou égal à zéro, on a :
$\displaystyle u_n(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}$ et $\displaystyle v_n(x)=u_n(x)+\frac{x^n}{n!}$
On en déduit que :
$\displaystyle u_n(0)=1+\frac{0}{1!}+\frac{0^2}{2!}+\cdots +\frac{0^n}{n!}=1$
Et de la même manière, on a :
$\displaystyle v_n(0)=u_n(0)+\frac{0^n}{n!}=1$
Finalement, on a $u_n(0)=1$ et $v_n(0)=1$.
2. Valeurs approchées à $10^{-6}$ près des termes de $u_n(x)$ pour $0\leq n\leq 10$ et pour les valeurs $1$, $2$ et $\sqrt{2}$ de $x$ :
Pour $x=1$, on a $\displaystyle u_n(1)=1+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}$
On en déduit que :
$u_0(1)=1$
$u_1(1)=1+\frac{1}{1!}=2$
$u_2(1)=1+\frac{1}{1!}+\frac{1}{2!}=2,5$
$u_3(1)=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}=2,666667$
$u_4(1)=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}=2,708333$
Et ainsi de suite … Ci-dessous les différentes valeurs synthétisées dans deux tableaux :
Pour $0\leq n\leq 5$ :
$$\large\begin{array}{|l|l|l|l|l|l|l|} \hline n=&0&1&2&3&4&5 \\ \hline n!=&1&1&2&6&24&120 \\ \hline u_n(x=1)&1&2&2,5&2,666667&2,708333&2,716667\\\hline u_n(x=2)&1&3&5&6,333333&7,000000&7,266667 \\ \hline u_n(x=\sqrt{2})&1&2,414214&3,414214&3,885618&4,052285&4,099425\\\hline\end{array}$$
Pour $6\leq n\leq 10$ :
$$\large\begin{array}{|L|L|l|l|l|l|} \hline n=&6&7&8&9&10 \\ \hline n!=&720&5040&40320&362880&3628800 \\ \hline u_n(x=1)&2,718056&2,718254&2,718279&2,718282&2,718282
\\\hline u_n(x=2)&7,355556&7,380952&7,387302&7,388713&7,388995 \\ \hline u_n(x=\sqrt{2})&4,110536&4,112781&4,113178&4,113240&4,113249\\\hline\end{array}$$
3. Conjecturer le comportement de la suite $(u_n)$ pour $x>0$ puis démontrer cette conjecture :
D’après les différentes valeurs calculées à la question précédente, on constate que la suite $(u_n)$ est croissante.
Pour démontrer ce résultat, calculons d’abord la différence de deux termes consécutifs.
Soient $p$ et $k$ deux entiers naturels et $x$ un réel strictement positif. On a :
$$\begin{align}u_{k+1}(x)-u_k(x)&=\sum_{p=0}^{k+1}\frac{x^p}{p!}-\sum_{p=0}^{k}\frac{x^p}{p!}\\&=\frac{x^{k+1}}{(k+1)!}\end{align}$$
Comme $x>0$, on peut conclure que $u_{k+1}(x)-u_k(x)>0$ puis que la suite $(u_n)$ est strictement croissante.
4. Une condition à satisfaire pour que la suite $(v_n)$ soit strictement décroissante, éventuellement à partir d’un certain rang :
On procède de la même manière que la question précédente, c’est à dire qu’on commence par calculer la différence entre deux termes consécutifs de la suite $(v_n)$.
Soient $p$ et $k$ deux entiers naturels et $x$ un réel strictement positif. On a :
$$\begin{align}v_{k+1}(x)-v_k(x)&=\left(\sum_{p=0}^{k+1}\frac{x^p}{p!}+\frac{x^{k+1}}{(k+1)!}\right)-\left(\sum_{p=0}^{k}\frac{x^p}{p!}+\frac{x^k}{k!}\right)\\&=\frac{2\,x^{k+1}}{(k+1)!}-\frac{x^k}{k!}\\&=\frac{(2x-(k+1))\,x^k}{(k+1)!}\end{align}$$
La suite $(v_n)$ est strictement décroissante si et seulement si on a $v_{k+1}(x)-v_k(x) < 0$ c’est à dire si $2x-(k+1) < 0$ ou encore $k > 2x-1$.
Calcul pour $x=4$ :
Pour $x=4$, la condition de décroissance de la $(v_n)$ établie ci-dessus nous donne $k>2\times 4 – 1$ soit $k>7$.
On doit donc constater que la suite $(v_n)$ décroit à partir du rang $n=8$.
Pour tout entier naturel $n$, on a :
$\displaystyle u_n(4)=1+\frac{4}{1!}+\frac{4^2}{2!}+\frac{4^3}{3!}+\cdots +\frac{4^n}{n!}$ et $\displaystyle v_n(4)=u_n(4)+\frac{4^n}{n!}$
On en déduit que,
$v_0(4)=u_0(4)+\frac{4^0}{0!}=1+1=2$
$v_1(4)=u_1(4)+\frac{4^1}{1!}=1+\frac{4}{1!}+4=1+4+4=9$
$v_2(4)=u_2(4)+\frac{4^2}{2!}=1+\frac{4}{1!}+\frac{4^2}{2!}+\frac{4^2}{2!}=5+4^2=21$
$\begin{align}v_3(4)&=u_2(4)+\frac{4^3}{3!}\\&=1+\frac{4}{1!}+\frac{4^2}{2!}+\frac{4^3}{3!}+\frac{4^3}{3!}\\&=5+8+2\times\frac{4^3}{6}\\&=13+\frac{4^3}{3}\\&=\frac{103}{3}\\&\sim 34,333333\end{align}$
Et ainsi de suite … Ci-dessous les différentes valeurs synthétisées dans un tableau :
$$\large\begin{array}{|l|l|l|l|l|l|l|} \hline n&0&1&2&3&4&5 \\ \hline v_n&2&9&21&34,333333&45&51,4\\\hline n&&6&7&8&9&10 \\ \hline v_n&&54,244444&55,05714&\color{red}{55,05714}&54,87654&54,73206\\\hline\end{array}$$
À travers le tableau ci-dessus, on constate que la suite $(v_n)$ est décroissante à partir du rang $n=8$.
5. Démontrer qu’avec la condition établie à la question précédente, les suites $(u_n)$ et $(v_n)$ sont adjacentes :
RAPPEL :
Pour montrer que les deux suite $(u_n)$ et $(v_n)$ sont adjacentes, il faut et il suffit de montrer que :
- Pour tout entier naturel $n$, $v_n > u_n$ (ou supérieure ou égale).
- $(u_n)$ est (strictement) croissante et $(v_n)$ est (strictement) décroissante.
- La limite $\displaystyle\lim_{n\to +\infty} (v_n(x)-u_n(x))=0$
Point 1 – $\forall n\in\mathbb{N}\,\,,\,v_n\geq u_n$ :
Pour tout entier naturel $n$ et pour tout réel $x$ strictement positif, on a :
$$v_n(x)=u_n(x)+\frac{x^n}{n!}$$
Soit,
$$v_n(x)-u_n(x)=\frac{x^n}{n!}>0$$
On en déduit que pour tout $n$ dans $\mathbb{N}$, $v_n> u_n$.
Point 2 – $(u_n)$ est strictement croissante et $(v_n)$ est strictement décroissante :
La stricte croissance de la suite $(u_n)$ a été démontrée à la question 3, puis à la question 4, il a été démontré que la suite $(v_n)$ est strictement décroissante à la condition $n>2x-1\,$.
Point 3 – La limite $\displaystyle\lim_{n\to +\infty} (v_n(x)-u_n(x))=0$ :
Pour montrer que la différence $\displaystyle v_n(x)-u_n(x)=\frac{x^n}{n!}$ converge vers zéro avec la condition $n>2x-1\,$, il suffit de montrer que la limite $\displaystyle\lim_{n\to +\infty}\frac{x^n}{n!}=0$.
Mais cette limite n’est pas simple à déterminer. Pour ce faire, on introduit la suite $(w_n)$ définie pour tout entier naturel $n$ et pour tout réel $x$ strictement positif par :
$$w_n(x)=v_n(x)-u_n(x)=\frac{x^n}{n!}$$
Pour tout $n$ dans $\mathbb{N}$ et pour tout $x$ dans $\mathbb{R}_+^*$, les termes de la suite $(w_n)$ sont strictement positifs et on peut donc évaluer le quotient $\displaystyle\frac{w_{n+1}(x)}{w_n(x)}$.
Ainsi, pour tout $n$ dans $\mathbb{N}$ et pour tout $x$ dans $\mathbb{R}_+^*$,
$$\begin{align}\frac{w_{n+1}(x)}{w_n(x)}&=\frac{x^{n+1}}{(n+1)!}\times\frac{n!}{x^n}\\&=\frac{x}{n+1}\end{align}$$
Or on sait que $n>2x-1$ donc,
$$\begin{align}n+1&>2x\\\frac{1}{2}&>\frac{x}{n+1}\\\frac{x}{n+1}&<\frac{1}{2}\end{align}$$
D’où,
$$\frac{w_{n+1}(x)}{w_n(x)}<\frac{1}{2}$$
Et par conséquent,
$$0<w_{n+1}(x)<\frac{1}{2}w_n(x)$$
Cette dernière égalité nous permet d’écrire une liste d’inégalité à partir de $n=0$,
$$0<w_{n}(x)<\frac{1}{2}w_{n-1}(x)$$
$$0<w_{n-1}(x)<\frac{1}{2}w_{n-2}(x)$$
$$\cdots$$
$$\cdots$$
$$0<w_{2}(x)<\frac{1}{2}w_1(x)$$
$$0<w_{1}(x)<\frac{1}{2}w_0(x)$$
Puisque les termes de la suite $(w_n)$ sont strictement positifs, le produit membre à membre de ces inégalités nous donne :
$$0 < w_1(x)\times w_2(x)\times\cdots\times w_{n-1}(x)\times w_n(x) < \frac{1}{2^n}\times w_0(x)\times w_1(x)\times\cdots\times w_{n-1}(x)$$
Puis en simplifiant par les termes identiques de part et d’autre nous donne pour tout $n$ dans $\mathbb{N}$ et pour tout réel $x$ dans $\mathbb{R}:
ATTENTION : Cette simplification sous-entend « division », elle est possible uniquement parce que les termes de la suite $(w_n)$ sont strictement positifs, donc différent de zéro.
$$0<w_n(x)<\frac{1}{2^n}w_0(x)$$
Comme la limite $\displaystyle\lim_{n\to +\infty}\frac{1}{2^n}=0$, alors $\displaystyle\lim_{n\to +\infty}w_n{x}=0$ d’après le théorème des gendarmes. On en déduit que la suite $(w_n)$ converge vers $0$.
Finalement, pour tout entier naturel $n$ on a $v_n > u_n$. De plus, la suite $(u_n)$ est strictement croissante, la suite $(v_n)$ est strictement décroissante pour $n>2x-1$, et $\displaystyle\lim_{n\to +\infty}v_n(x)-u_n(x)=0$. On peut donc affirmer que les deux suites $(u_n)$ et $(v_n)$ sont adjacentes et qu’elles convergent vers la même limite $\ell_x$.
6. En examinant les termes successifs obtenus dans la question 1 pour $x=1$, conjecturer la valeur de $\ell_1$. Quelle généralisation est suggérée en examinant les valeurs de $\ell_x$ pour $x=2$ et $x=\sqrt{2}$ ?
D’après le tableau de valeurs de la question 1, on a $u_10(1)=2,718282$ à $10^{-6}$ près. Cette valeur est identique à celle de $e$ pour les cinq premières décimales. On peut donc conjecturer que $\ell_1=e$.
Ensuite, on a $u_10(2)=7,3890$ à $10^{-4}$ près. Cette valeur est identique à celle de $e^2$ pour les quatre premières décimales. On peut donc conjecturer que $\ell_2=e^2$.
Enfin, on a $u_10(\sqrt{2})=4,113249$ à $10^{-6}$ près et $\displaystyle e^{\sqrt{2}}\sim 4,113250$ à $10^{-6}$ près.
Ces constats nous poussent à conjecturer que $\ell_x=e^x$.
PARTIE II
1. On pose $I_n(x)=\frac{1}{u_n(x)}$.
1.a. Valeurs de $I_n(x)$ pour $x=1$ et $x=2$ et $0\leq n\leq 10$ :
Valeurs de $I_n(1)$ pour $0\leq n\leq 10$ :
$$\large\begin{array}{|l|l|l|l|l|l|l|} \hline n&0&1&2&3&4&5 \\ \hline \frac{1}{u_n}&1&0,5&0,4&0,375&0,369231&0,368098\\\hline n&&6&7&8&9&10 \\ \hline \frac{1}{u_n}&&0,36791&0,367883&0,367883&0,367879&0,367879\\\hline\end{array}$$
Valeurs de $I_n(2)$ pour $0\leq n\leq 10$ :
$$\large\begin{array}{|l|l|l|l|l|l|l|} \hline n&0&1&2&3&4&5 \\ \hline \frac{1}{u_n}&1&0,33&0,2&0,157895&0,142857&0,137615\\\hline n&&6&7&8&9&10 \\ \hline \frac{1}{u_n}&&0,135952&0,135484&0,135367&0,135342&0,135336\\\hline\end{array}$$
1.b. Quelle conjecture peut-on émettre suite à l’observation des résultats obtenus ?
D’après le tableau de valeurs ci-dessus, on a $I_{10}(1)=0,367879$ à $10^{-6}$ près. Cette valeur est identique à celle de $e^{-1}$ à $10^{-6}$ près. De même, on a $I_{10}(2)=0,13533$ à $10^{-5}$ qui est une valeur approchée de $e^{-2}$ à $10^{-5}$ près.
On peut donc conjecturer que la suite $(I_n)$ converge vers $e^{-x}$.
2. Représentations graphiques :
Les polynômes considérés sont :
$u_1(x)=1+x\,$, $u_2(x)=1+x+\frac{x^2}{2}\,$, $u_3(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}\,$, $u_4(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}\,$ et $u_5(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}$
$v_1(x)=1+2x\,$, $v_2(x)=1+x+x^2\,$, $v_3(x)=1+x+\frac{x^2}{2}+\frac{x^3}{3}\,$, $v_4(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{12}\,$ et $v_5(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{60}$
Les courbes correspondant aux polynômes $u$ sont en bleu, celles correspondant aux polynômes $v$ sont en rouge.
$u_1$ et $v_1$ :
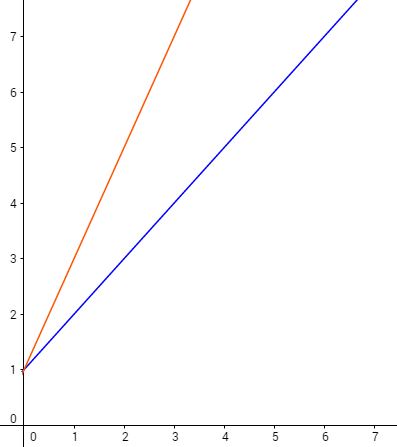
$u_2$ et $v_2$ :
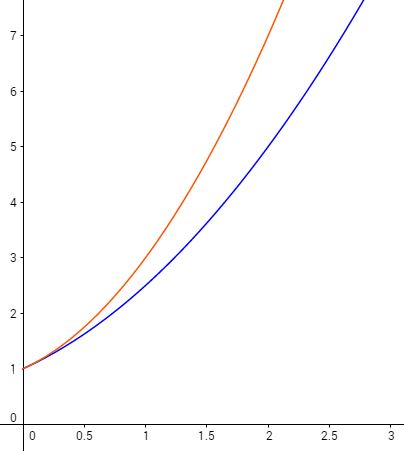
$u_3$ et $v_3$ :
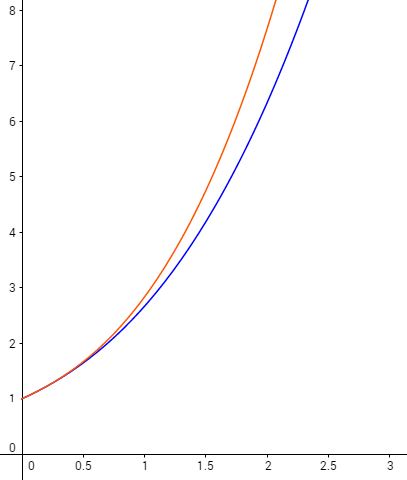
$u_4$ et $v_4$ :
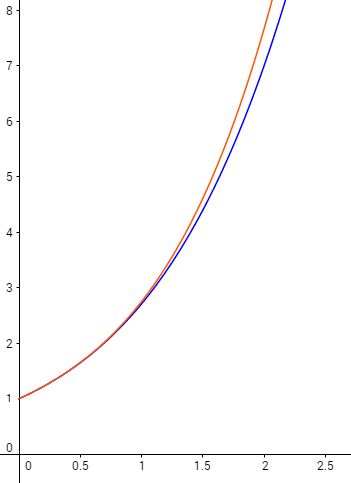
$u_5$ et $v_5$ :

Quelle conjecture est suggérée par l’examen de ces courbes ?
L’examen de ces courbes suggère qu’elles encadrent de plus en plus près la courbe représentative de la fonction $x\mapsto e^x$.
3. Calcul de la dérivée de la fonction $u_n$ et relation entre celle-ci et $u_{n-1}$ :
$n$ est un entier naturel.
La fonction $u_n$ est définie pour tout réel $x$ supérieur ou égal à zéro par :
$$u_n(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots +\frac{x^n}{n!}$$
$u_n$ est fonction polynomiale donc dérivable sur $\mathbb{R}$ et pour tout entier naturel $n$ et tout réel $x$ supérieur ou égal à zéro on a :
$$\begin{align}u_n^{\prime}(x)&=0+1+\frac{2x}{2}+\frac{3x}{6}+\cdots +\frac{n\,x^{n-1}}{n!}\\&=1+\frac{x}{1}+\frac{x}{2!}+\cdots +\frac{x^{n-1}}{(n-1)!}\\&=\sum_{p=0}^{n-1}\frac{x^p}{p!}\\&=u_{n-1}(x)\end{align}$$
Quelle indice supplémentaire concernant la convergence de la suite $(u_n)$ cette relation suggère-t-elle ?
On peut conjecturer que la fonction limite $\displaystyle\lim_{n\to +\infty}\sum_{p=0}^{n}\frac{x^p}{p!}$ et sa dérivée sont égales.
Dans le cadre du programme de la terminale, cela reste une conjecture car rien ne nous dit que ce qui est vrai pour $x$ réel est vrai lorsque $x$ tend vers $+\infty$. Il s’agit cependant d’un indice supplémentaire car on sait que la fonction $x\mapsto e^x$ est dérivable sur $\mathbb{R}$ et que sa dérivée est elle-même, i.e $x\mapsto e^x$.
PARTIE III
L’objet de cette partie est de démontrer que $\ell_1$ est irrationnel.
1. On suppose que $\displaystyle\ell_1=\frac{p}{q}$ où $p$ et $q$ sont deux entiers strictement positifs. Déterminer un encadrement de $\ell_1$ en fonction de $u_q(1)$ et de $q$.
$\ell_1$ est la limite commune pour $x=1$ des suites adjacentes $(u_n)$ et $(v_n)$.
De plus $(u_n)$ est strictement croissante et $(v_n)$ est strictement décroissante, on a donc l’encadrement suivant :
$$u_n(1) < \ell_1 < v_n(1)$$
D’où,
$$u_q(1) <\ell_1 < v_q(1)$$
Où encore,
$$u_q(1) <\ell_1 < u_q(1)+\frac{1}{q!}$$
2. Conclusion :
L’idée ici est de montrer que $\ell_1$ est irrationnel en raisonnant par l’absurde.
On suppose que $\ell_1$ est un nombre rationnel, c’est à dire qu’il existe deux entiers strictement positifs $p$ et $q$ tels que $\displaystyle\ell_1=\frac{p}{q}$.
On a donc,
$\begin{align}u_q(1)&=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots +\frac{1}{(q-1)!}+\frac{1}{q!}\\&=\frac{q!}{q!}+\frac{q!}{q!}+\frac{3\times 4\times\cdots\times q}{q!}+\frac{4\times 5\times\cdots\times q}{q!}+\cdots +\frac{q}{q!}+\frac{1}{q!}\\&=\frac{q!+q!+3\times 4\times\cdots\times q+4\times 5\times\cdots\times q+q+1}{q!}\\&=\frac{N}{q!}\end{align}$
où $N$ est un entier car somme de produits d’entiers.
À l’aide de l’encadrement établi dans la question précédente, on a :
$$\frac{N}{q!} < \frac{p}{q} < \frac{N}{q!}+\frac{1}{q!}$$
Soit en multipliant tous les membres par $q!$,
$$N<q!\times\frac{p}{q} < N+1$$
Puis,
$$N<(q-1)!\times p < N+1$$
Par conséquent $(q-1)!\times p$ est un nombre entier compris strictement (Il s’agit ici d’inégalités strictes) entre deux entiers consécutifs ($N$ et $N+1$), ce qui est impossible.
On en conclut donc que l’hypothèse de départ est fausse. $\ell_1$ n’est donc pas un nombre rationnel.
Il s’agit d’un indice supplémentaire qui va dans dans le sens des différentes conjectures émises tout au long de ce problème, car on sait (ou pas
) que $e^1$ est irrationnel.
FIN
Je suis ingénieur télécoms de formation et j’exerce ce métier depuis toujours. Je reste cependant passionné par les mathématiques et très proche de ce domaine.
À travers mathsland, je m’enrichis chaque jour au contact de personnes remarquables, passionnées et passionnantes.