Théorème des valeurs intermédiaires, continuité

Soient $a$ et $b$ deux réels tels que $a\neq b$ et $f$ l’application de $\displaystyle [a\,;\,b]$ dans $\displaystyle [a\,;\,b]$ définie par :

 

$$\begin{cases}f\left([a\,;\,b]\subset [a\,;\,b]\right)\\\\\forall (x\,;\,y)\in [a\,;\,b]\times [a\,;\,b]\,,\quad|f(x)-f(y)|<|x-y|\end{cases}$$

 

1. Montrer que $f$ est continue sur $\displaystyle [a\,;\,b]$.

2. Soit $g$ la fonction définie pour tout réel $x$ de $\displaystyle [a\,;\,b]$ par :

$$g(x)=f(x)-x$$

2.1 Montrer que $g$ est strictement décroissante sur $\displaystyle [a\,;\,b]$.

2.2 Déterminer le signe de $g(a)g(b)$.

3. En déduire qu’il existe un unique réel $\alpha$ appartenant à $\displaystyle [a\,;\,b]$ tel que $f(\alpha)=\alpha$.

 

FIN

Vous trouverez dans cet onglet des indications pour aborder les passages délicats ou particulièrement difficiles de cet exercice

 

$a$ et $b$ sont deux réels tels que $a\neq b$ et $f$ est l’application de $\displaystyle [a\,;\,b]$ dans $\displaystyle [a\,;\,b]$ définie par :

$$\begin{cases}f\left([a\,;\,b]\subset [a\,;\,b]\right)\\\\\forall (x\,;\,y)\in [a\,;\,b]\times [a\,;\,b]\,,\quad|f(x)-f(y)|<|x-y|\end{cases}$$

 

Question 1 :

Montrer que $f$ est continue sur $\displaystyle [a\,;\,b]$ :

Pour répondre rigoureusement à cette question, il faudra connaître la définition de la continuité sur un intervalle fermé.

CONTINUITÉ SUR UN INTERVALLE – RAPPEL :

Soient $a$ et $b$ deux réels et soit $f$ une fonction définie sur l’intervalle $\displaystyle [a\,;\,b]$.

Conventionnellement, on dit que $f$ est continue sur l’intarvalle $\displaystyle [a\,;\,b]$ si les trois conditions suivantes sont vérifiées :

(1) $f$ est continue en tout point de l’intervalle ouvert $\displaystyle ]a\,;\,b[$

(2) $f$ est continue à droite de $a$, c’est à dire que $\displaystyle\lim_{x\to a^+}f(x)=f(a)$

(3) $f$ est continue à gauche de $b$, c’est à dire que $\displaystyle\lim_{x\to b^-}f(x)=f(b)$

(Naturellement, les limites $\displaystyle\lim_{x\to a^+}f(x)$ et $\displaystyle\lim_{x\to b^-}f(x)$ doivent exister )

Puis, il faudra montrer que $f$ vérifie chacune de ces trois hypothèses.

 

Une autre méthode consiste à utiliser la définition de la continuité avec les quantificateurs (méthode connue aussi sous le nom de « epsilon-delta »), mais tout le monde n’est pas à l’aise avec cette méthode

 

Question 2.1 :

$g$ est la fonction définie pour tout réel $x$ de $\displaystyle [a\,;\,b]$ par :

$$g(x)=f(x)-x$$

Montrer que $g$ est strictement décroissante sur l’intervalle $\displaystyle [a\,;\,b]$ :

Il faudra évaluer le taux d’accroissement de $g$ : $\displaystyle\frac{g(x)-g(y)}{x-y}$ pour $x$ et $y$ deux éléments distincts de $\displaystyle [a\,;\,b]$ puis montrer que ce taux d’accroissement est strictement négatif.

 

Question 3 :

Existence d’un unique réel $\alpha$ appartenant à $\displaystyle [a\,;\,b]$ tel que $f(\alpha)=\alpha$ :

La formulation de la question suggère d’utiliser le corollaire du théorème des valeurs intermédiaires (connu également sous le nom du théorème de la bijection).

Rappel du corollaire du théorème des valeurs intermédiaires (T.V.I) :

Soit $f$ une fonction définie, continue et strictement monotone sur un intervalle $\displaystyle [a\,;\,b]$.

Alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$, l’équation $f(x)=k$ admet une solution unique dans $\displaystyle [a\,;\,b]$.

Vous pouvez par exemple commencer par appliquer ce théorème à la fonction $g$ dont nous connaissons la stricte monotonie …

 

FIN

$a$ et $b$ sont deux réels tels que $a\neq b$ et $f$ est l’application de $\displaystyle [a\,;\,b]$ dans $\displaystyle [a\,;\,b]$ définie par :

$$\begin{cases}f\left([a\,;\,b]\subset [a\,;\,b]\right)\\\\\forall (x\,;\,y)\in [a\,;\,b]\times [a\,;\,b]\,,\quad|f(x)-f(y)|<|x-y|\end{cases}$$

 

1. $f$ est continue sur $\displaystyle [a\,;\,b]$ :

Pour répondre à cette question, il faudra utiliser la définition de la continuité sur un intervalle fermé.

CONTINUITÉ SUR UN INTERVALLE – RAPPEL :

Soient $a$ et $b$ deux réels et soit $f$ une fonction définie sur l’intervalle $\displaystyle [a\,;\,b]$.

Conventionnellement, on dit que $f$ est continue sur l’intarvalle $\displaystyle [a\,;\,b]$ si les trois conditions suivantes sont vérifiées :

(1) $f$ est continue en tout point de l’intervalle ouvert $\displaystyle ]a\,;\,b[$

(2) $f$ est continue à droite de $a$, c’est à dire que $\displaystyle\lim_{x\to a^+}f(x)=f(a)$

(3) $f$ est continue à gauche de $b$, c’est à dire que $\displaystyle\lim_{x\to b^-}f(x)=f(b)$

(Naturellement, les limites $\displaystyle\lim_{x\to a^+}f(x)$ et $\displaystyle\lim_{x\to b^-}f(x)$ doivent exister )

 

Ainsi, si on démontre que $f$ vérifie les trois points ci-dessus, on pourra conclure que $f$ est continue sur l’intervalle $\displaystyle [a\,;\,b]$.

(1) $f$ est continue en tout point de l’intervalle ouvert $\displaystyle ]a\,;\,b[$ :

Soit $x_0$ un élément de $\displaystyle ]a\,;\,b[$.

D’après la définition de $f$, on a :

$$\forall x\in [a\,;\,b]\,,\quad|f(x)-f(x_0)|<|x-x_0|$$

C’est à dire,

$$\forall x\in [a\,;\,b]\,,\quad 0\leq |f(x)-f(x_0)|<|x-x_0|$$

Puisque,

$$\lim_{x\to x_0}|x-x_0|=0$$

Alors d’après le théorème des gendarmes,

$$\lim_{x\to x_0}|f(x)-f(x_0)|=0$$

Et par suite,

$$\lim_{x\to x_0}f(x)=f(x_0)$$

On en déduit que $f$ est continue pour tout réel $x_0$ de $\displaystyle ]a\,;\,b[$. $f$ est donc continue sur $\displaystyle ]a\,;\,b[$.

 

(2) $f$ est continue à droite de $a$, c’est à dire que $\displaystyle\lim_{x\to a^+}f(x)=f(a)$ :

On utilise à nouveau la définition de $f$ et on a :

$$\forall x\in [a\,;\,b]\,,\quad|f(x)-f(a)|<|x-a|$$

Puisque,

$$\lim_{x\to a^+}|x-a|=0$$

Alors d’après le théorème des gendarmes,

$$\lim_{x\to a^+}|f(x)-f(a)|=0$$

Et par suite,

$$\lim_{x\to a^+}f(x)=f(a)$$

$f$ est donc continue à droite de $a$.

 

(3) $f$ est continue à gauche de $b$, c’est à dire que $\displaystyle\lim_{x\to b^-}f(x)=f(b)$

Pour ce faire, il suffit de procéder de la même façon que pour la continuité à droite de $a$.

En effet, on a,

$$\forall x\in [a\,;\,b]\,,\quad|f(x)-f(a)|<|x-a|$$

Puisque,

$$\lim_{x\to b^-}|x-b|=0$$

Alors d’après le théorème des gendarmes,

$$\lim_{x\to b^-}|f(x)-f(b)|=0$$

Et par suite,

$$\lim_{x\to b^-}f(x)=f(b)$$

$f$ est donc continue à gauche de $b$.

Finalement, $f$ est continue sur l’intervalle $\displaystyle [a\,;\,b]$.

 

REMARQUE :

Une autre méthode consiste à utiliser la définition de la continuité avec les quantificateurs (connue aussi sous le nom de « epsilon-delta »), mais tout le monde n’est pas à l’aise avec cette méthode

Soit $x_0$ dans $\displaystyle [a\,;\,b]$.

Pour $\epsilon >0$, il existe un $\delta=\epsilon >0$ tel que :

$$\forall x\in [a\,;\,b]\;,\;|x-x_0|\leq\delta=\epsilon\,\Rightarrow\,|f(x)-f(x_0)|<|x-x_0|\leq\epsilon$$

Cela montre que $f$ est continue en $x_0$ , pour tout $x_0$ dans $\displaystyle [a\,;\,b]$, $f$ est donc continue sur $\displaystyle [a\,;\,b]$.

 

2. Soit $g$ la fonction définie pour tout réel $x$ de $\displaystyle [a\,;\,b]$ par :

$$g(x)=f(x)-x$$

2.1 $g$ est strictement décroissante sur $\displaystyle [a\,;\,b]$ :

L’idée ici est d’évaluer le taux d’accroissement de $g$ : $\displaystyle\frac{g(x)-g(y)}{x-y}$ pour $x$ et $y$ deux éléments distincts de $\displaystyle [a\,;\,b]$ et de montrer que ce taux d’accroissement est strictement négatif.

Soient $x$ et $y$ deux réels distincts de $\displaystyle [a\,;\,b]$.

Le taux d’accroissement de $g$ s’écrit :

$$\begin{align}\frac{g(x)-g(y)}{x-y}&=\frac{f(x)-x-(f(y)-y)}{x-y}\\&=\frac{f(x)-f(y)-(x-y)}{x-y}\\&=\frac{f(x)-f(y)}{x-y}-1\end{align}$$

Or d’après la définition de $f$, on a pour tous réels $x$ et $y$ dans $\displaystyle [a\,;\,b]$ :

$$|f(x)-f(y)|<|x-y|$$

Comme dans cette question on a $x\neq y$, alors on peut écrire :

$$\left|\frac{f(x)-f(y)}{x-y}\right|<1$$

Et on en déduit que,

$$\frac{g(x)-g(y)}{x-y}<0$$

$g$ est donc strictement décroissante sur $\displaystyle [a\,;\,b]$.

 

2.2 Signe de $g(a)g(b)$ :

On commence par évaluer la quantité $g(a)g(b)$.

On a,

$$g(a)g(b)=(f(a)-a)(f(b)-b)$$

On sait d’après la question 1 que $f$ est continue sur $\displaystyle [a\,;\,b]$, et on on sait d’après la définition de $f$ que $\displaystyle f\left([a\,;\,b]\subset [a\,;\,b]\right)$. Ce que l’on peut illustrer avec le graphique suivant :

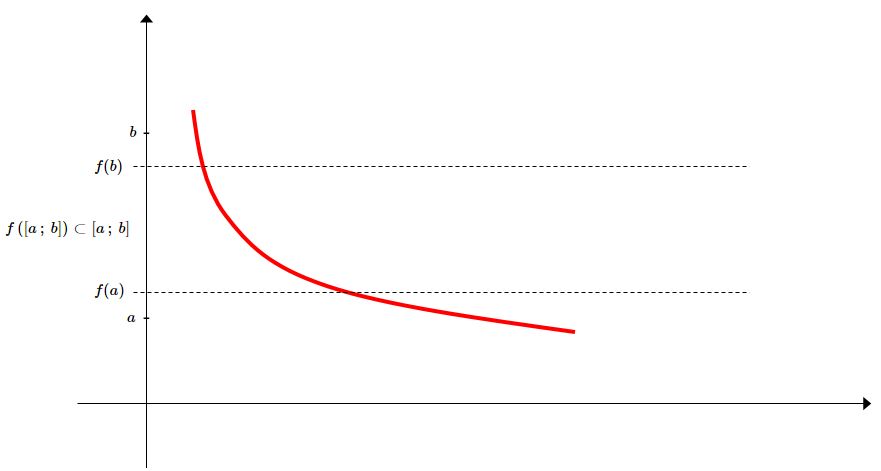
On voit aisément que le fait d’avoir $\displaystyle f\left([a\,;\,b]\subset [a\,;\,b]\right)$ implique $a\leq f(a)$ et $f(b)\leq b$ et par suite $f(a)-a\geq 0$ et $f(b)-b\leq 0$.

Finalement, $g(a)g(b)\leq 0$.

 

3. Existence d’un unique réel $\alpha$ dans $\displaystyle [a\,;\,b]$ tel que $f(\alpha)=\alpha$ :

La façon dont cette question est formulée suggère l’utilisation du corollaire du théorème des valeurs intermédiaires (connu également sous le nom du théorème de la bijection).

Rappel du corollaire du théorème des valeurs intermédiaires (T.V.I) :

Soit $f$ une fonction définie, continue et strictement monotone sur un intervalle $\displaystyle [a\,;\,b]$.

Alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$, l’équation $f(x)=k$ admet une solution unique dans $\displaystyle [a\,;\,b]$.

Ici, il faudra commencer d’abord par appliquer ce corollaire à $g$ dont on connaît la stricte monotonie (question 2.1).

On sait que $f$ est continue sur $\displaystyle [a\,;\,b]$, donc $g$ est continue sur $\displaystyle [a\,;\,b]$ comme somme de deux fonctions continues sur $\displaystyle [a\,;\,b]$.

Puisque $g$ est strictement décroissante sur $\displaystyle [a\,;\,b]$, alors $g$ réalise une bijection de $\displaystyle [a\,;\,b]$ vers $\displaystyle [g(b)\,;\,g(a)]$.

De plus, on a montré à la question 2.b que $g(a)g(b)\leq 0$, on en déduit que $\displaystyle 0\in [a\,;\,b]$.

Et par suite, d’après le corollaire du théorème des valeurs intermédiaires, l’équation $g(x)=0$ admet une unique solution dans $\displaystyle [a\,;\,b]$, autrement dit, il existe un unique réel $\displaystyle\alpha\in [a\,;\,b]$ tel que $g(\alpha)=0$.

Finalement, comme $\displaystyle g(\alpha)=f(\alpha)-\alpha$, alors il existe un unique réel $\displaystyle\alpha\in [a\,;\,b]$ tel que $f(\alpha)=\alpha\,$.

 

FIN